2023-09-13 · Clippin and Ceilin
Contents
2023-09-13 · Clippin and Ceilin¶
include("lib/Nto1.jl")
using Revise … ✔ (0.3 s)
using Units, Nto1AdEx, ConnectionTests, ConnTestEval, MemDiskCache … ✔ (0.6 s)
using StatsBase … ✔ (0.3 s)
N = 6500
duration = 10minutes
@time sim = Nto1AdEx.sim(N, duration, ceil_spikes = false);
2.988527 seconds (2.10 M allocations: 1.024 GiB, 2.50% gc time, 44.07% compilation time)
(Hm, spikerate not 4.0 Hz (even though we use our lookup table))
sim.spikerate / Hz
4.7
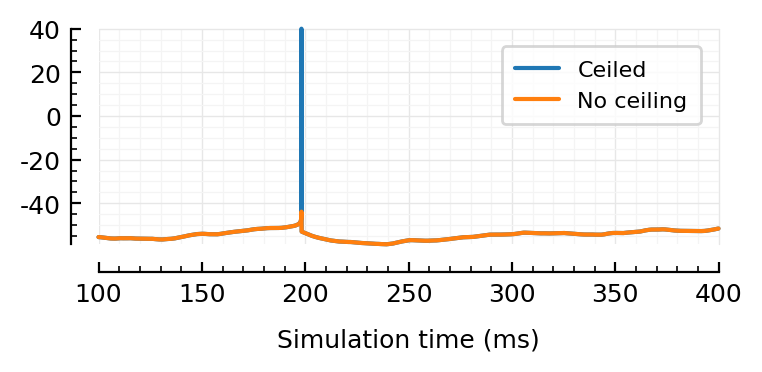
Ceil¶
V_no_ceil = sim.V;
V_ceil = ceil_spikes!(copy(V_no_ceil), sim.spiketimes); # V_ceil = Vₛ =
Nto1AdEx.Vₛ / mV
40
include("lib/plot.jl")
import PythonCall … ✔ (2.2 s)
import PythonPlot … ✔ (5.9 s)
using Sciplotlib … [ Info: Precompiling Sciplotlib [88be95e5-9550-4d5f-a203-92a5acbc3118]
✔ (3.9 s)
using PhDPlots … [ Info: Precompiling PhDPlots [8882fb83-7a18-4ae0-b3ef-a58e1f4042a1]
✔ (2.4 s)
fig, ax = plt.subplots(figsize=(4, 1.4))
plotsig(V_ceil / mV, [100, 400], ms, label="Ceiled")
plotsig(V_no_ceil / mV, [100, 400], ms, label="No ceiling")
legend(ax, reverse=false);
Clip¶
And now for the clipping, we do it data driven (i.e. no explicit spike detection), just a percentile.
include("lib/df.jl")
using DataFrames … ✔ (1 s)
set_print_precision(4)
ENV["DATAFRAMES_ROWS"] = 12;
ps = [0, 0.1, 1, 5, 10, 50, 90, 95, 99, 99.9, 99.95, 99.99, 100]
qs = percentile(V_ceil, ps)
df = DataFrame("p" => ps, "V (mV)" => qs/mV)
showsimple(df)
p V (mV)
────────────────
0 -65
0.1 -58.75
1 -58.07
5 -57.37
10 -56.91
50 -53.98
90 -51.6
95 -51.06
99 -49.79
99.9 -46.77
99.95 -44.24
99.99 40
100 40
df_ = permutedims(df, "p", strict=false)
showsimple(df_, allcols=true)
p 0.0 0.1 1.0 5.0 10.0 50.0 90.0 95.0 99.0 99.9 99.95 99.99 100.0
──────────────────────────────────────────────────────────────────────────────────────────────────────────
V (mV) -65 -58.75 -58.07 -57.37 -56.91 -53.98 -51.6 -51.06 -49.79 -46.77 -44.24 40 40
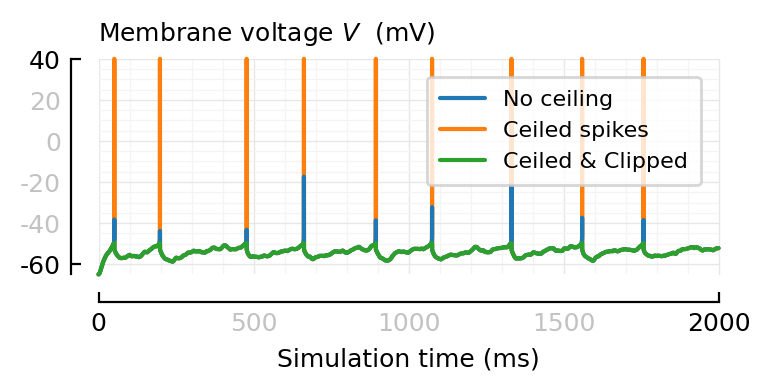
Okay, lesgo for 99.
clip!(V, p = 99) = begin
V_thr = percentile(V, p)
to_clip = V .≥ V_thr
V[to_clip] .= V_thr
V
end
V_ceil_n_clip = clip!(copy(V_ceil));
Vs = [
(V = V_no_ceil, label = "No ceiling", zorder = 2),
(V = V_ceil, label = "Ceiled spikes", zorder = 1),
(V = V_ceil_n_clip, label = "Ceiled & Clipped", zorder = 3),
];
function plot_ceil_n_clip_sigs(ax=newax(); kw...)
for (V, label, zorder) in Vs
plotsig(V, [0, 2000], ms; label, zorder, yunit=:mV, yunits_in=nothing, ax, kw...)
end
hylabel(ax, L"Membrane voltage $V$ (mV)")
deemph_middle_ticks(ax)
legend(ax)
end
fig, ax = plt.subplots(figsize=(4, 1.4))
plot_ceil_n_clip_sigs(ax);
STAs¶
exc_input_1 = highest_firing(excitatory_inputs(sim))[1]
SpikeTrain(58522 spikes, 97.54 Hz, [0.004668, 0.01482, 0.04501, 0.04727, 0.05836, 0.07584, 0.0927, 0.1063, 0.1094, 0.1099 … 599.9, 600, 600, 600, 600, 600, 600, 600, 600, 600])
ConnectionTests.set_STA_length(100ms);
function plot_ceil_n_clip_STAs(ax=newax(); legend_=true)
# set(ax, ylim=[-54.1601, -54.02]) # grr (no work)
for (V, label, zorder) in Vs
STA = calc_STA(V, exc_input_1.times)
plotSTA(STA; label, nbins_y=4, hylabel=nothing, yunits_in=nothing, ax)
end
hylabel(ax, L"Spike-triggered average (STA) of $V$ (mV)")
deemph_middle_ticks(ax)
legend_ && legend(ax)
end
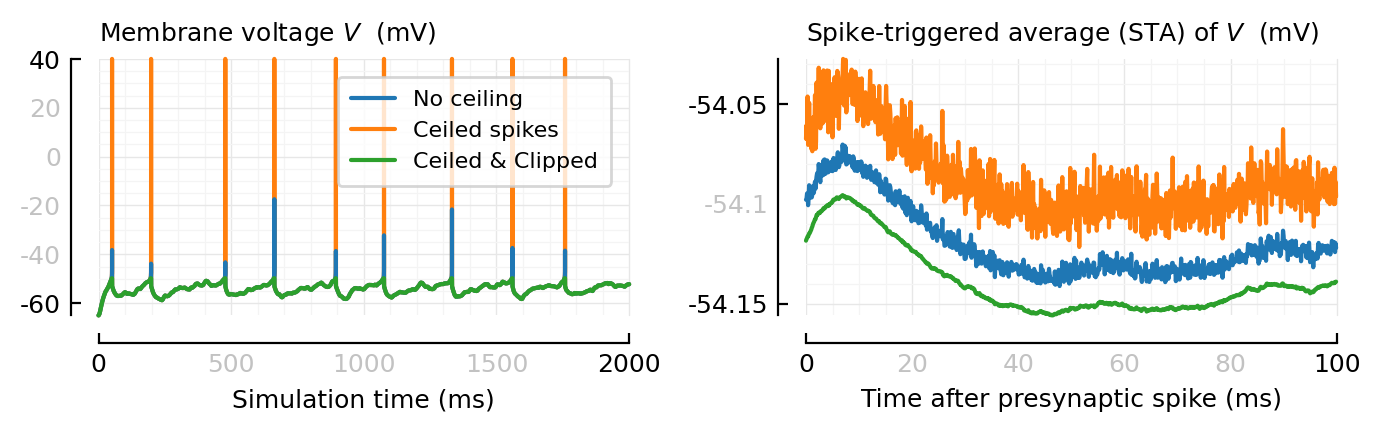
plot_ceil_n_clip_STAs();
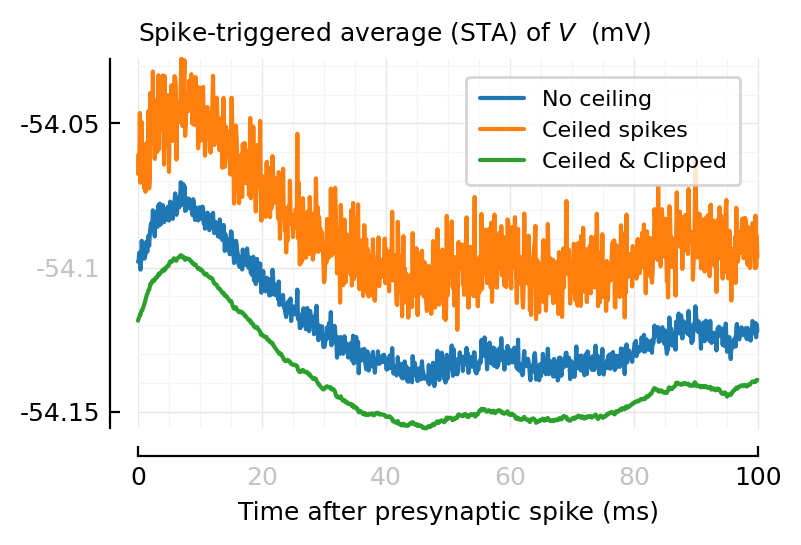
Interesting! They have diff base heights (very convenient for plotting on same ax, here).
Ok, it makes sense. They’re averages: each sample dragged down or up.
Together now.
fig, axs = plt.subplots(ncols=2, figsize=(cw, 0.32cw))
plot_ceil_n_clip_sigs(axs[0], xlabel="Simulation time")
plot_ceil_n_clip_STAs(axs[1], legend_=false)
plt.tight_layout();
savefig_phd("ceil_n_clip__sigs_and_STAs")
Saved at `../thesis/figs/ceil_n_clip__sigs_and_STAs.pdf`
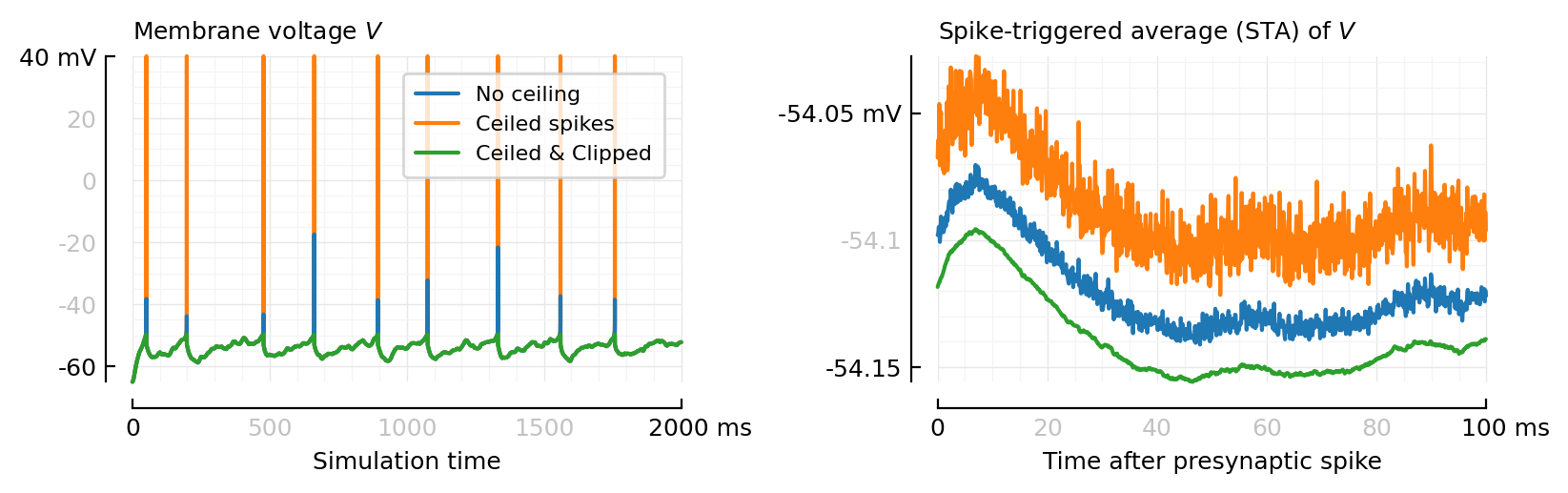
fig, axs = plt.subplots(ncols=2, figsize=(pw, 0.32pw))
plot_ceil_n_clip_sigs(axs[0], xlabel="Simulation time")
plot_ceil_n_clip_STAs(axs[1], legend_=false)
plt.tight_layout();
savefig_phd("ceil_n_clip__sigs_and_STAs")
Saved at `../thesis/figs/ceil_n_clip__sigs_and_STAs.pdf`
ROCs¶
trains_to_test = get_trains_to_test(sim);
ConnectionTests.set_STA_length(20ms);
function test_conns(V)
test(train) = test_conn(STAHeight(), V, train.times)
rows = []
for (conntype, trains) in trains_to_test
descr = string(conntype)
@showprogress descr for train in trains
t = test(train)
fr = spikerate(train)
push!(rows, (; conntype, fr, t))
end
end
DataFrame(rows)
end;
MemDiskCache.set_dir("2023-09-13__Clippin_and_Ceilin")
"C:\\Users\\tfiers\\.julia\\MemDiskCache.jl\\2023-09-13__Clippin_and_Ceilin"
df_no_ceil = @cached test_conns(V_no_ceil); # 55.6 seconds
Loading [C:\Users\tfiers\.julia\MemDiskCache.jl\2023-09-13__Clippin_and_Ceilin\test_conns(V_no_ceil).jld2] … ✔ (2.6 s)
df_ceil = @cached test_conns(V_ceil); # 51.3 seconds
Loading [C:\Users\tfiers\.julia\MemDiskCache.jl\2023-09-13__Clippin_and_Ceilin\test_conns(V_ceil).jld2] … ✔
df_ceil_n_clip = @cached test_conns(V_ceil_n_clip); # 51.8 seconds
Loading [C:\Users\tfiers\.julia\MemDiskCache.jl\2023-09-13__Clippin_and_Ceilin\test_conns(V_ceil_n_clip).jld2] … ✔
dfs = [df_no_ceil, df_ceil, df_ceil_n_clip];
sweeps = sweep_threshold.(dfs)
AUCs = calc_AUROCs.(sweeps);
labels = extract(:label, Vs);
df = DataFrame(AUCs)
insertcols!(df, 1, :V_type=>labels)
showsimple(df)
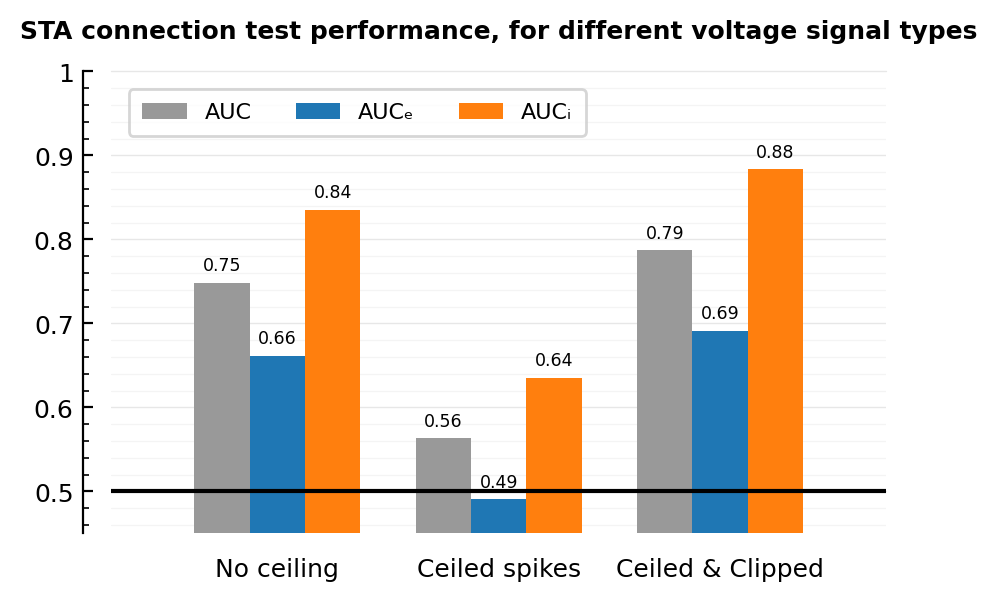
V_type AUC AUCₑ AUCᵢ
──────────────────────────────────────────
No ceiling 0.7485 0.6617 0.8354
Ceiled spikes 0.5632 0.4909 0.6354
Ceiled & Clipped 0.7874 0.6912 0.8836
Distilling from mpl docs’ Examples: Grouped bar chart with labels:
function grouped_barplot(df; cols, group_labels, ax=nothing, bar_label_fmt="%.2g", colors=nothing, kw...)
N_groups = length(group_labels)
N_bars_per_group = length(cols)
if isnothing(ax)
fig, ax = plt.subplots()
end
if isnothing(colors)
colors = mplcolors[1:N_bars_per_group]
end
x = 0:(N_groups - 1)
width = 1/(N_bars_per_group + 1)
for (i, (colname, color)) in enumerate(zip(cols, colors))
values = df[!, colname]
offset = (i-1) * width
bars = ax.bar(x .+ offset, values, width, label=colname, color=toRGBAtuple(color))
ax.bar_label(bars, padding = 3, fmt=bar_label_fmt, fontsize="x-small")
end
set(ax, xtype=:categorical)
ax.set_xticks(x .+ width, group_labels)
return ax
end
fig, ax = plt.subplots(figsize=(5, 3))
ax.axhline(0.5, color="black")
colors = [color_both, color_exc, color_inh]
ax = grouped_barplot(df, cols=["AUC", "AUCₑ", "AUCᵢ"], group_labels=df.V_type; ax, colors);
legend(ax, ncols=3, loc="upper left")
set(ax, ylim=[0.45, 1], xtype=:keep, title="""
STA connection test performance, for different voltage signal types""");
savefig_phd("ceil_n_clip_AUCs")
Saved at `../thesis/figs/ceil_n_clip_AUCs.pdf`
Threshold-plot¶
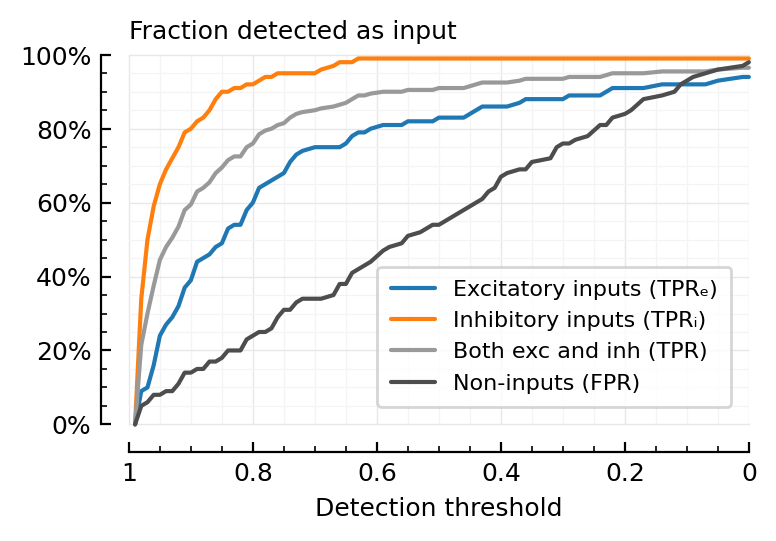
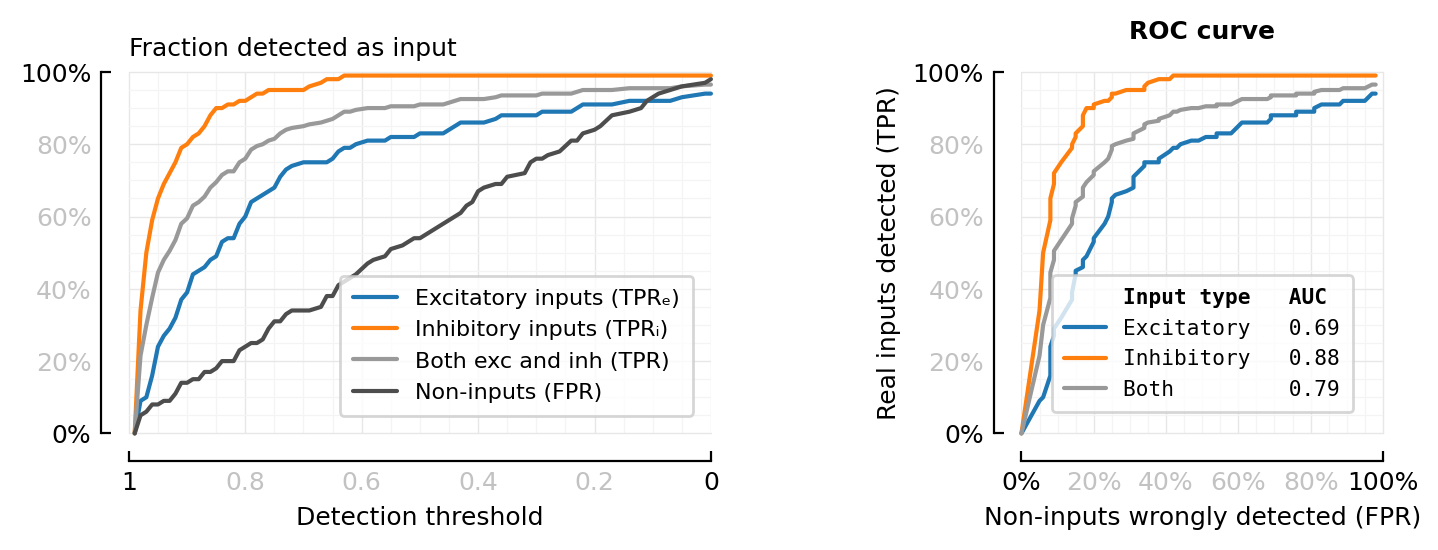
Visualize what ROC is.
sweep = sweep_threshold(df_ceil_n_clip);
function plot_perfmeasures_threshold_TPRs(ax=newax())
plot(sweep.threshold, sweep.TPRₑ; color=color_exc, label="Excitatory inputs (TPRₑ)", ax)
plot(sweep.threshold, sweep.TPRᵢ; color=color_inh, label="Inhibitory inputs (TPRᵢ)", ax)
plot(sweep.threshold, sweep.TPR; color=color_both, label="Both exc and inh (TPR)", ax)
plot(sweep.threshold, sweep.FPR; color=color_unconn, label="Non-inputs (FPR)", ax)
set(ax, ytype=:fraction, hylabel="Fraction detected as input", xlabel="Detection threshold")
ax.invert_xaxis()
legend(ax)
end
plot_perfmeasures_threshold_TPRs();
fig, axs = plt.subplots(ncols=2, figsize=(0.92pw, 0.34pw))
plot_perfmeasures_threshold_TPRs(axs[0])
plotROC(sweep; ax=axs[1])
deemph_middle_ticks(fig);
axs[1].set_title("ROC curve")
plt.tight_layout(w_pad=4)
savefig_phd("perfmeasures_θ_TPR_ROC")
Saved at `../thesis/figs/perfmeasures_θ_TPR_ROC.pdf`
Precision & F-scores¶
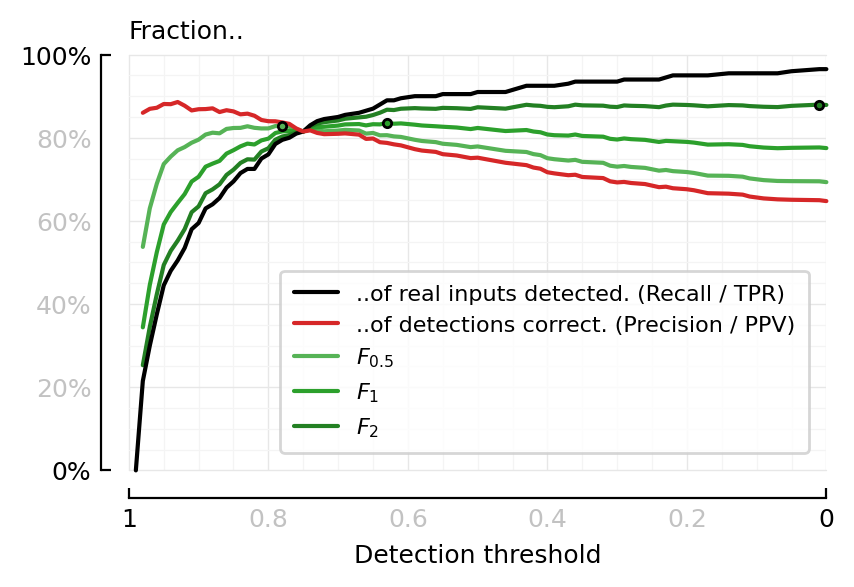
function plot_perfmeasures_Fscores(ax=newax())
plot(sweep.threshold, sweep.TPR; color=black, label="..of real inputs detected. (Recall / TPR)", ax, zorder=2)
plot(sweep.threshold, sweep.PPV; color=C3, label="..of detections correct. (Precision / PPV)", ax, zorder=2)
for (series, color, label) in [
(sweep.F05, lighten(C2), L"F_{0.5}"),
(sweep.F1, C2, L"F_1"),
(sweep.F2, darken(C2), L"F_2"),
]
plot(sweep.threshold, series; color, label, ax, zorder=1)
i = argmax(skipnan(series))
plot(sweep.threshold[i], series[i], "."; color, mec="black", ax, zorder=3)
end
set(ax, ytype=:fraction, xlabel="Detection threshold", hylabel="Fraction..")
ax.invert_xaxis()
deemph_middle_ticks(ax)
legend(ax)
# label_lines(ax, yoffset=[2=>-0.02])
end
fig, ax = plt.subplots(figsize=(mtw, 0.6*mtw))
plot_perfmeasures_Fscores(ax)
savefig_phd("perfmeasures_Fscores");
Saved at `../thesis/figs/perfmeasures_Fscores.pdf`
using PythonCall: pyconvert
function label_lines(ax; yoffset=[])
offsets = Dict(offsets)
for (i, line) in enumerate(ax.lines)
x,y = pyconvert(NTuple{2,Vector{Float64}}, line.get_data())
s = pyconvert(String, line.get_label())
dy = get(offset, i, 0)
ax.text(x[end], y[end]+dy, " $s", color=line.get_color(), va="center", fontsize="small")
end
end;
# Very cool.
# Not using now though :) Just the normal legend.
#
# To possibly add: allow specifying offset in axes coords;
# so need to add to diff transforms (I did this before for sth else).
Where is F1 maximal?
PR curve (analogous to ROC):
(note, in ROC, recall (TPR) is on y; here it’s on x)
“Out of all that’s predicted [inh], how many actually are”.
Iso-Fβ curves¶
Iso-Fβ curves :) (msc throwback).
So, a formula to isolate precision from F formula.
⪅(x,y) = (x < y) || x ≈ y;
precision(recall, F; β) = begin
P = (
(recall * F)
/
( (1+β^2)*recall - β^2*F )
)
return (0 ⪅ P ⪅ 1) ? P : NaN
end;
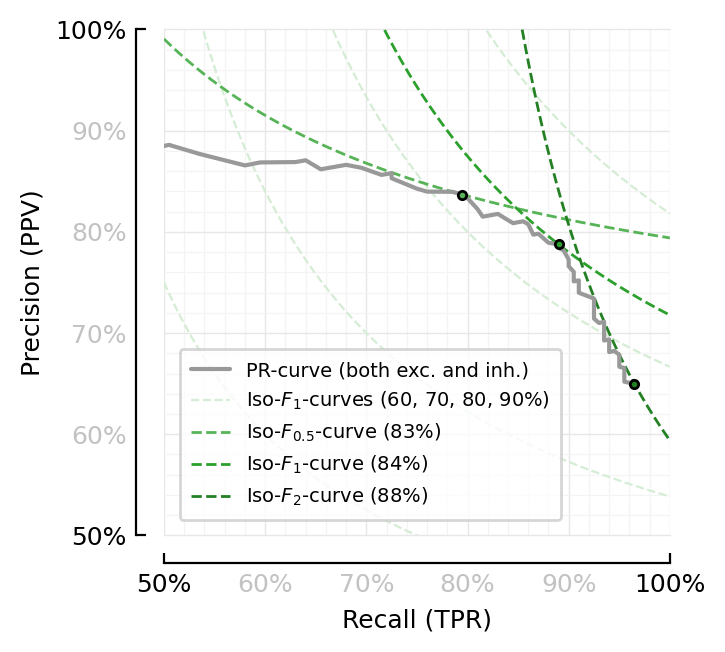
function plot_perfmeasures_PR_curves_iso_Fβ(ax=newax())
plot(sweep.TPR, sweep.PPV; color=color_both, ax, label="PR-curve (both exc. and inh.)", clip_on=true)
x0 = 0.5
R = x0:(1/1000):1
Fs = [0.6, 0.7, 0.8, 0.9]
Fs_str = join(100*Fs, ", ") * "%"
for (i,F) in enumerate(Fs)
label = (i > 1) ? nothing : L"Iso-$F_1$-curves (%$Fs_str)"
plot(R, precision.(R, F; β=1); color=lighten(C2,0.2), lw=0.8, ls="--", clip_on=true, zorder=1, label, ax)
end
for (β, series, color) in [
(β=0.5, series=sweep.F05, color= lighten(C2)),
(β=1, series=sweep.F1, color=identity(C2)),
(β=2, series=sweep.F2, color= darken(C2)),
]
F, i = findmax(skipnan(series))
label=L"Iso-$F_{%$β}$-curve (%$(round(100*F))%)"
plot(R, precision.(R, F; β); ax, color, lw=1, ls="--", label, clip_on=true, zorder=1)
plot(sweep.recall[i], sweep.precision[i], "."; mec="black", mfc=color, zorder=2, ax)
end
# set(ax, title=("""
# Performance of STA test for
# different input detection thresholds""", :fontsize=>"small"))
set(ax, aspect="equal", xtype=:fraction, ytype=:fraction,
xlabel="Recall (TPR)", ylabel="Precision (PPV)",
xlim=[x0, 1], ylim=[x0, 1])
deemph_middle_ticks(ax)
legend(ax, fontsize=7, loc="lower left")
end
fig, ax = plt.subplots(figsize=fs(0.73mtw, 1))
plot_perfmeasures_PR_curves_iso_Fβ(ax)
savefig_phd("PR_curves_iso_Fβ");
Saved at `../thesis/figs/PR_curves_iso_Fβ.pdf`
Both together now.
fig, axs = plt.subplot_mosaic([
[".", "B"],
["A", "B"],
[".", "B"],
], figsize=(0.9pw, 0.5cw), width_ratios=[1.5, 1], height_ratios=[1,99999,1])
plot_perfmeasures_Fscores(axs["A"])
plot_perfmeasures_PR_curves_iso_Fβ(axs["B"])
fig.tight_layout(w_pad=5);
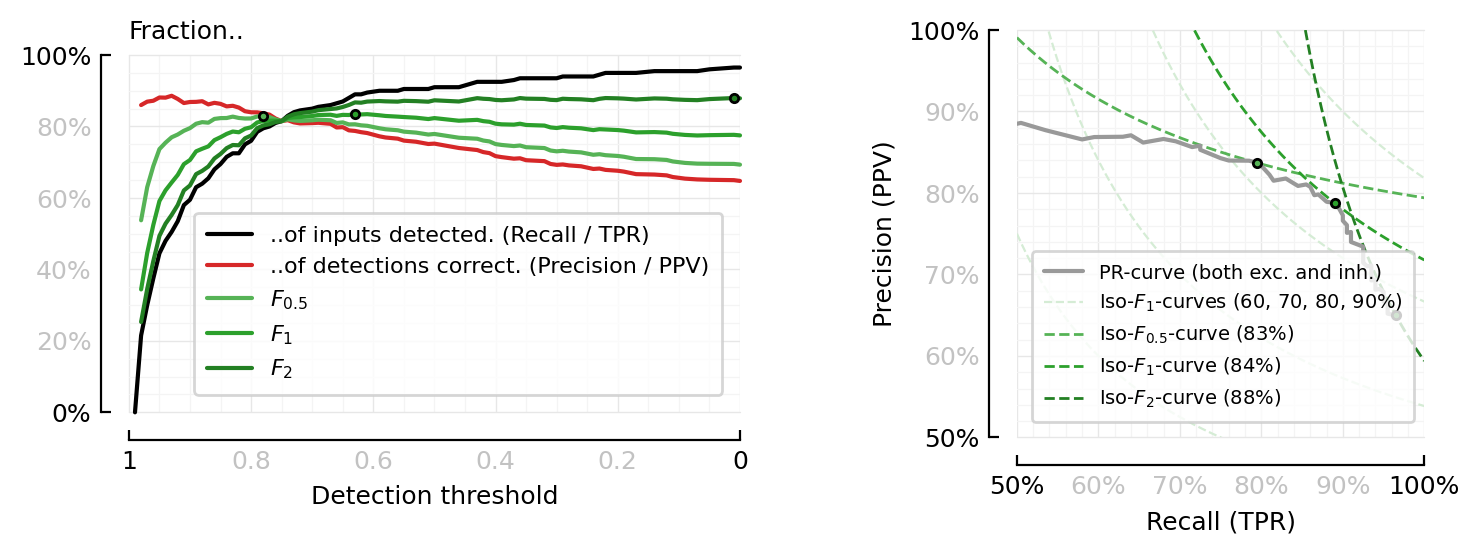
Eh, too much to digest at once. Better separate.
We don’t want too many R points (for smaller fig filesize).
We wanna know where precision(R) == 1.
(To selectively add these points to our x (R) linspace :). For nice near-asympote plotting).
I.e. solve: R = …
Picking up from above and continuing (on a diff branch): $$ \begin{align}
β^2 P F &= PR + β^2 PR - R F \[0.8em]
R &= \frac{β^2 P F}{P + β^2 P - F}\[0.8em]
R &= \frac{β^2 P F}{(1 + β^2)P - F}\[0.8em]
\end{align} $$
recall(precision, F; β) = begin
R = (
(β^2 * precision * F)
/
( (1+β^2)*precision - F )
)
return (0 ⪅ R ⪅ 1) ? R : NaN
end;
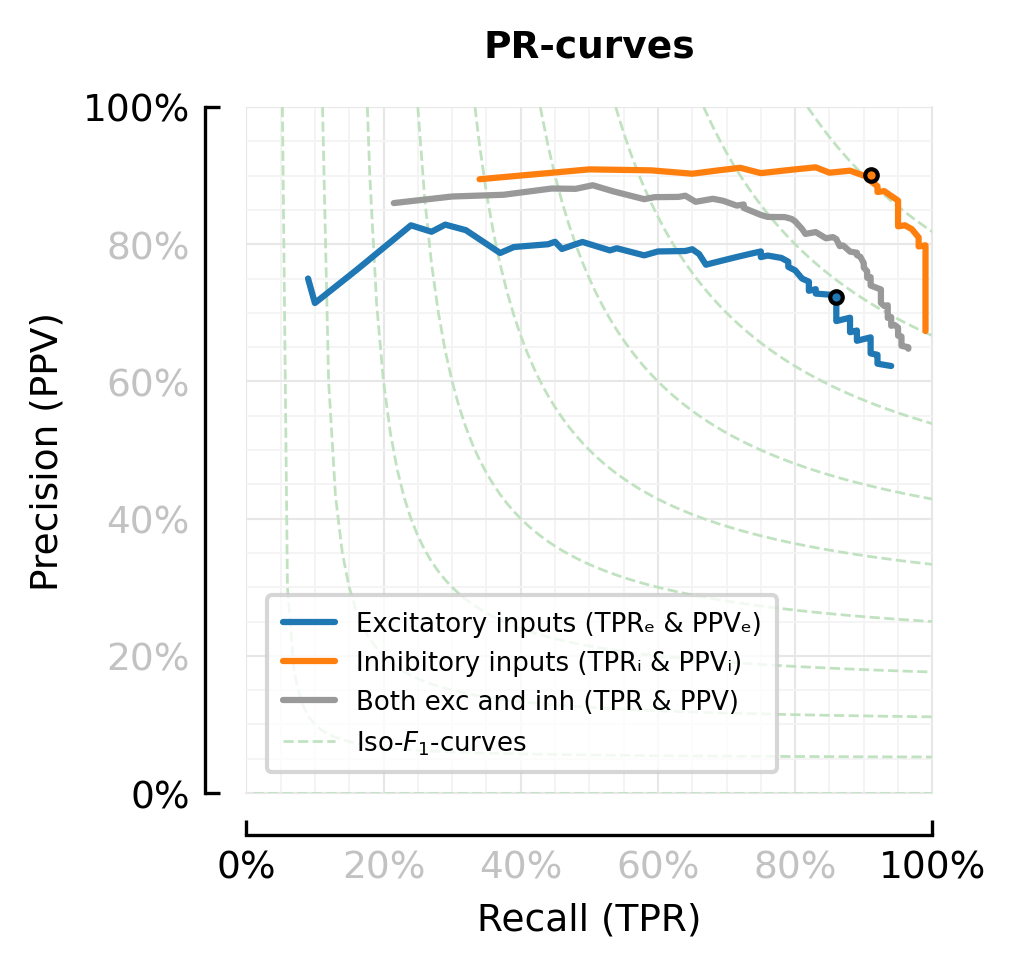
function plot_perfmeasures_PR_curves_EI(ax)
plot(sweep.TPRₑ, sweep.PPVₑ; color=color_exc, ax, label="Excitatory inputs (TPRₑ & PPVₑ)")
plot(sweep.TPRᵢ, sweep.PPVᵢ; color=color_inh, ax, label="Inhibitory inputs (TPRᵢ & PPVᵢ)")
plot(sweep.TPR, sweep.PPV ; color=color_both, ax, label="Both exc and inh (TPR & PPV)")
iₑ = argmax(skipnan(sweep.F1ₑ))
plot(sweep.TPRₑ[iₑ], sweep.PPVₑ[iₑ], "."; color=color_exc, mec="black")
iᵢ = argmax(skipnan(sweep.F1ᵢ))
plot(sweep.TPRᵢ[iᵢ], sweep.PPVᵢ[iᵢ], "."; color=color_inh, mec="black")
β = 1
Fs = 0:0.1:1
R = 0:(1/100):1
extra_Rs = recall.(1, Fs; β)
R = sort!([R..., extra_Rs...])
for (i,F) in enumerate(Fs)
label = (i > 1) ? nothing : L"Iso-$F_1$-curves"
P = precision.(R, F; β)
plot(R, P; color=lighten(C2, 0.3), lw=0.66, ls="--", clip_on=true, zorder=1, label)
end
set(ax, aspect="equal", xtype=:fraction, ytype=:fraction,
xlabel="Recall (TPR)", ylabel="Precision (PPV)")
legend(ax, fontsize="x-small", loc="lower left")
end
fig, ax = plt.subplots(figsize=fs(0.66mtw, 1), dpi=300)
plot_perfmeasures_PR_curves_EI(ax)
deemph_middle_ticks(fig)
ax.set_title("PR-curves")
savefig_phd("perfmeasures_PR_curves_EI");
Saved at `../thesis/figs/perfmeasures_PR_curves_EI.pdf`
Two thresholds?¶
“Do we need two thresholds?” i.e. one for exc and one for inh. (pfrt)
deemph_(t, color="gray") = t.set_color("gray")
legend_label_texts(ax) = pyconvert(Vector, ax.legend_.get_texts());
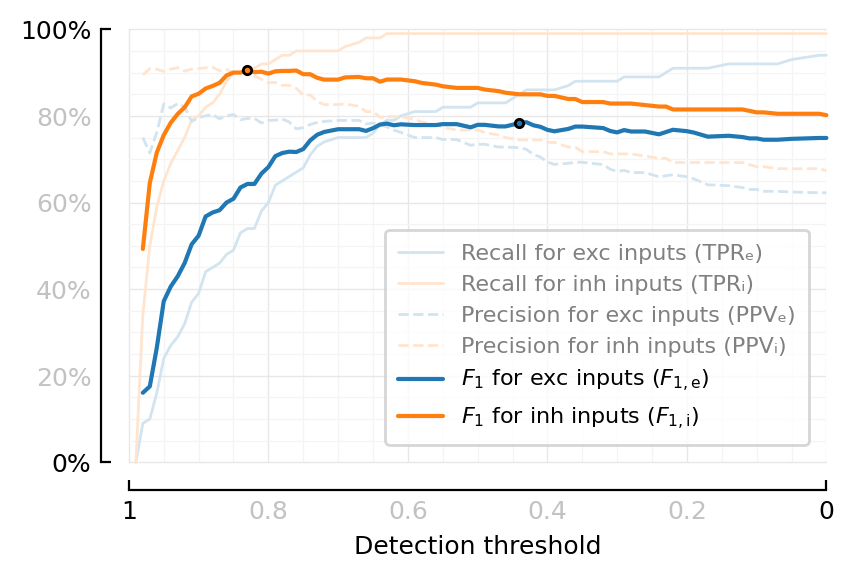
function plot_perfmeasures_threshold_PPVs_EI(ax=newax())
θ = sweep.threshold
plot(θ, sweep.TPRₑ; color=lighten(color_exc,.2), lw=1, ax, label="Recall for exc inputs (TPRₑ)")
plot(θ, sweep.TPRᵢ; color=lighten(color_inh,.2), lw=1, ax, label="Recall for inh inputs (TPRᵢ)")
plot(θ, sweep.PPVₑ; color=lighten(color_exc,.2), lw=1, ax, label="Precision for exc inputs (PPVₑ)", ls="--")
plot(θ, sweep.PPVᵢ; color=lighten(color_inh,.2), lw=1, ax, label="Precision for inh inputs (PPVᵢ)", ls="--")
plot(θ, sweep.F1ₑ; color=color_exc, ax, label=L"$F_1$ for exc inputs ($F_{1,\mathrm{e}}$)")
plot(θ, sweep.F1ᵢ; color=color_inh, ax, label=L"$F_1$ for inh inputs ($F_{1,\mathrm{i}}$)")
iₑ = argmax(filter(!isnan, sweep.F1ₑ))
plot(θ[iₑ], sweep.F1ₑ[iₑ], "."; color=color_exc, mec="black")
iᵢ = argmax(skipnan(sweep.F1ᵢ))
plot(θ[iᵢ], sweep.F1ᵢ[iᵢ], "."; color=color_inh, mec="black")
set(ax, ytype=:fraction, xlabel="Detection threshold")
ax.invert_xaxis()
legend(ax);
deemph_.(legend_label_texts(ax)[1:4])
end
fig, ax = plt.subplots(figsize=fs(mtw, 1.6))
plot_perfmeasures_threshold_PPVs_EI(ax)
deemph_middle_ticks(fig)
savefig_phd("perfmeasures_threshold_PPVs_EI");
Saved at `../thesis/figs/perfmeasures_threshold_PPVs_EI.pdf`
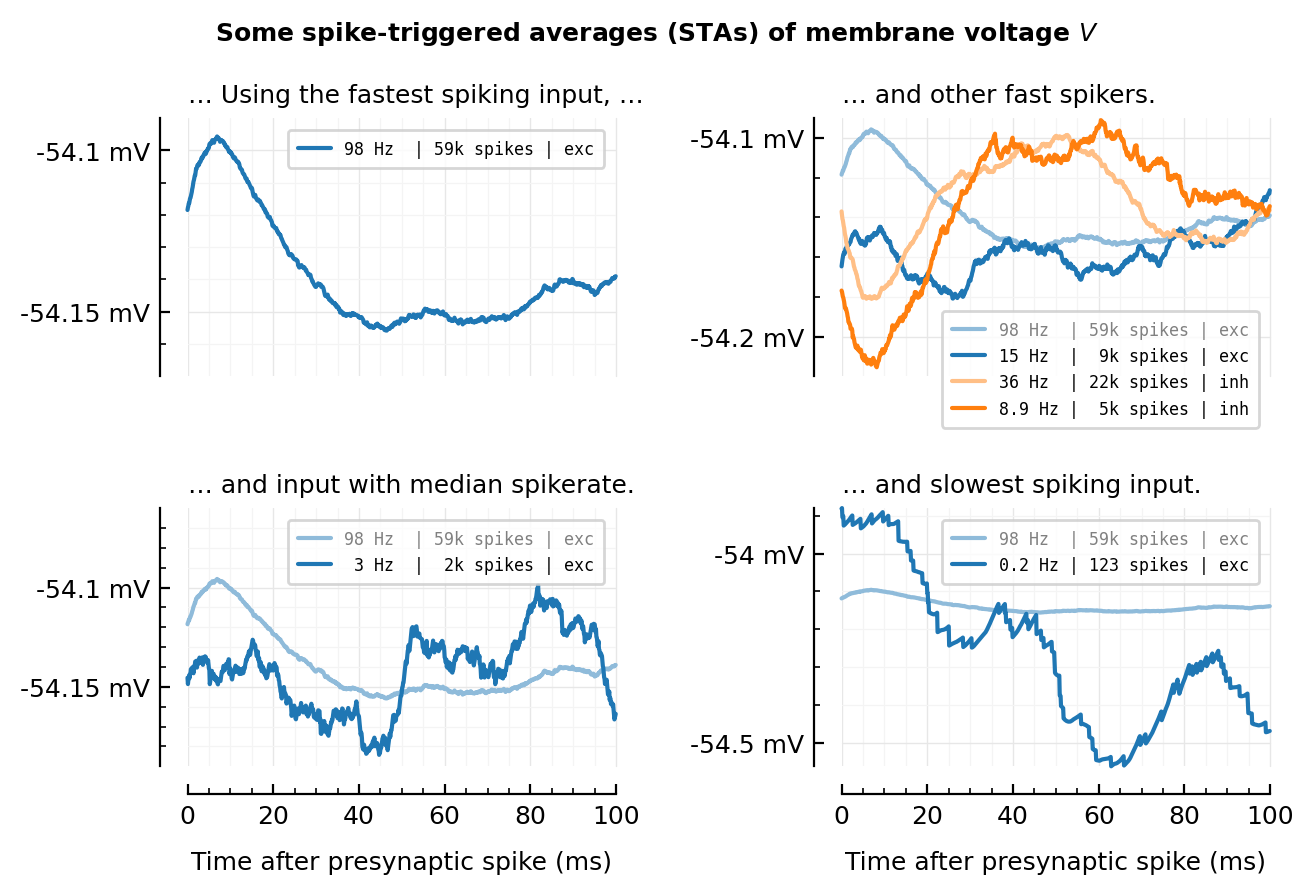
STA examples plot¶
(repeat of 2023-08-30__STA_examples, but now with clipped spikes, i.e. cleaner; and what we – in the end – actually use for the conntests :)).
ConnectionTests.set_STA_length(100ms);
V = V_ceil_n_clip
exc_inputs = highest_firing(excitatory_inputs(sim))
inh_inputs = highest_firing(inhibitory_inputs(sim))
mid = length(exc_inputs) ÷ 2
plotSTA_(train; hylabel=nothing, xlim=[0,100], yunit_in=:every_ticklabel, kw...) = begin
n = num_spikes(train)
if n ≥ 1000
n = string(round(Int, n / 1000)) * "k"
end
r = round(spikerate(train), sigdigits=2)
if isinteger(r)
r = Int(r)
end
r = "$(lpad(r,2)) Hz"
exc_or_inh = (train ∈ exc_inputs) ? "exc" : "inh"
label = "$(rpad(r, 6)) | $(lpad(n,3)) spikes | $exc_or_inh"
plotSTA(calc_STA(V, train.times); label, hylabel, xlim, nbins_y=3, yunit_in, kw...)
end;
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(pw*0.8, mtw))
addlegend(ax; kw...) = legend(
ax, borderaxespad=0.7, prop=Dict("family"=>"monospace", "size"=>6); kw...)
ax = axs[0,0]
xkw = (xlabel=nothing, xunit_in=nothing)
plotSTA_(exc_inputs[1]; ax, hylabel="… Using the fastest spiking input, …", xkw..., ylim=[-54.17, -54.09]);
rm_ticks_and_spine(ax, "bottom")
addlegend(ax)
ax = axs[0,1]
plotSTA_(exc_inputs[1]; ax, color=lighten(color_exc, 0.5), xkw..., hylabel="… and other fast spikers.")
plotSTA_(exc_inputs[100]; ax, color=lighten(color_exc, 1.0), xkw...)
plotSTA_(inh_inputs[1]; ax, color=lighten(color_inh, 0.5), xkw...)
plotSTA_(inh_inputs[100]; ax, color=lighten(color_inh, 1.0), xkw..., ylim=[-54.22, -54.09])
rm_ticks_and_spine(ax, "bottom")
addlegend(ax, bbox_to_anchor=(1, 0.3), loc="upper right")
deemph_(first(legend_label_texts(ax)))
ax = axs[1,1]
plotSTA_(exc_inputs[1]; ax, hylabel="… and slowest spiking input.", color=lighten(color_exc, 0.5))
plotSTA_(exc_inputs[end]; ax, color=lighten(color_exc, 1.0))
addlegend(ax)
deemph_(first(legend_label_texts(ax)))
ax = axs[1,0]
plotSTA_(exc_inputs[1]; ax, hylabel="… and input with median spikerate.", color=lighten(color_exc, 0.5))
plotSTA_(exc_inputs[mid]; ax, ylim=[-54.19, -54.06], color=lighten(color_exc, 1.0))
addlegend(ax, loc="upper right")
deemph_(first(legend_label_texts(ax)))
plt.suptitle(L"Some spike-triggered averages (STAs) of membrane voltage $V$", size="medium")
plt.tight_layout(h_pad=2.5, w_pad=2);
savefig_phd("example_STAs")
Saved at `../thesis/figs/example_STAs.pdf`