2022-04-28 • Interpolate N = 30 .. 6000
Contents
2022-04-28 • Interpolate N = 30 .. 6000¶
The N = 30 case had a fixed firing rate for the input neurons (of 20 Hz).
We’ll now also give it the lognormal (with mean 4 Hz) firing rate distribution.
We must introduce a new concept / parameter: the desired stimulation rate of the input neurons. It is a product of average firing rate and ‘stimulation’ (synaptic conductance increase, Δg) per spike. Given that average spike rate is fixed (namely 4 Hz), we use this paramter to calculate Δg.
A sensible value for it is taken from the previous (N = 6600) notebook where Δg_exc was 0.4 nS and the Δg_multiplier was 0.066.
We’ll thus choose avg_stimulation_rate__exc to be 0.4 nS * 0.066 * 4 Hz, or 0.1 nS/second.
Our inhibitory inputs have 4x the strength, so avg_stimulation_rate__inh will be 0.4 nS/second.
The actual stimulation rate for each input neuron will vary from these, as their firing rates are not 4 Hz, but rather distributed lognormally somewhere around that.
Params¶
N_excs = [
4, # => N_inh = 1
17, # Same as in `previous_N_30_input`.
80,
320,
1280,
5200,
];
get_params(N_exc) = ExperimentParams(
sim = SimParams(
duration = 10 * minutes,
imaging = get_VI_params_for(cortical_RS, spike_SNR = Inf),
input = PoissonInputParams(; N_exc),
),
);
param_sets = get_params.(N_excs);
dumps(param_sets[1])
ExperimentParams
rngseed: 22022022
sim: SimParams
duration: 600.0
Δt: 0.0001
num_timesteps: 6000000
rngseed: 0
input: PoissonInputParams
N_unconn: 100
N_exc: 4
N_inh: 1
N_conn: 5
N: 105
spike_rates: LogNormal
μ: 1.08629
σ: 0.774597
synapses: SynapseParams
avg_stim_rate_exc: 1.0e-10
avg_stim_rate_inh: 4.0e-10
E_exc: 0.0
E_inh: -0.065
g_t0: 0.0
τ: 0.007
izh_neuron: IzhikevichParams
C: 1.0e-10
k: 7.0e-7
v_rest: -0.06
v_thr: -0.04
a: 30.0
b: -2.0e-9
v_peak: 0.035
v_reset: -0.05
Δu: 1.0e-10
v_t0: -0.06
u_t0: 0.0
imaging: VoltageImagingParams
spike_SNR: Inf
spike_SNR_dB: Inf
spike_height: 0.095
σ_noise: 0.0
conntest: ConnTestParams
STA_window_length: 0.1
num_shuffles: 100
rngseed: 22022022
evaluation: EvaluationParams
α: 0.05
num_tested_neurons_per_group: 40
rngseed: 22022022
Run¶
perfs = Vector()
for params in param_sets
@show params.sim.input.N_conn
perf = performance_for(params)
@show perf
push!(perfs, perf)
println()
end
params.sim.input.N_conn = 5
Running simulation: 100%|███████████████████████████████| Time: 0:00:14
perf = (TPR_exc = 1.0, TPR_inh = 1.0, FPR = 0.07499999999999996)
params.sim.input.N_conn = 21
Running simulation: 100%|███████████████████████████████| Time: 0:00:12
perf = (TPR_exc = 1.0, TPR_inh = 1.0, FPR = 0.0)
params.sim.input.N_conn = 100
Running simulation: 100%|███████████████████████████████| Time: 0:00:12
perf = (TPR_exc = 1.0, TPR_inh = 0.85, FPR = 0.0)
params.sim.input.N_conn = 400
Running simulation: 100%|███████████████████████████████| Time: 0:00:18
perf = (TPR_exc = 0.925, TPR_inh = 0.425, FPR = 0.09999999999999998)
params.sim.input.N_conn = 1600
Running simulation: 100%|███████████████████████████████| Time: 0:00:45
perf = (TPR_exc = 0.525, TPR_inh = 0.225, FPR = 0.050000000000000044)
params.sim.input.N_conn = 6500
Running simulation: 100%|███████████████████████████████| Time: 0:02:32
perf = (TPR_exc = 0.05, TPR_inh = 0.5, FPR = 0.15000000000000002)
Plot results¶
import PyPlot
using VoltageToMap.Plot
xlabels = [p.sim.input.N_conn for p in param_sets]
xticks = [1:length(xlabels);]
plot_detection_rate(detection_rate; kw...) = plot(
xticks,
detection_rate,
".-";
ylim=(0, 1),
xminorticks=false,
clip_on=false,
kw...
)
ax = plot_detection_rate([p.TPR_exc for p in perfs], label="for excitatory inputs")
plot_detection_rate([p.TPR_inh for p in perfs], label="for inhibitory inputs")
plot_detection_rate([p.FPR for p in perfs], label="for unconnected spikers")
@unpack α = param_sets[1].evaluation
ax.axhline(α, color="black", zorder=3, lw=1, linestyle="dashed", label=f"α = {α:.3G}")
# We don't use our `set`, as that undoes our `xminorticks=false` command (bug).
ax.set_xticks(xticks, xlabels)
ax.set_xlabel("Number of connected inputs")
ax.yaxis.set_major_formatter(PyPlot.matplotlib.ticker.PercentFormatter(xmax=1))
ax.xaxis.grid(false)
ax.tick_params(bottom=false)
ax.spines["bottom"].set_visible(false)
l = ax.legend(title="Detection rate", ncol=2, loc="lower center", bbox_to_anchor=(0.5, 1.1));
l._legend_box.align = "left";
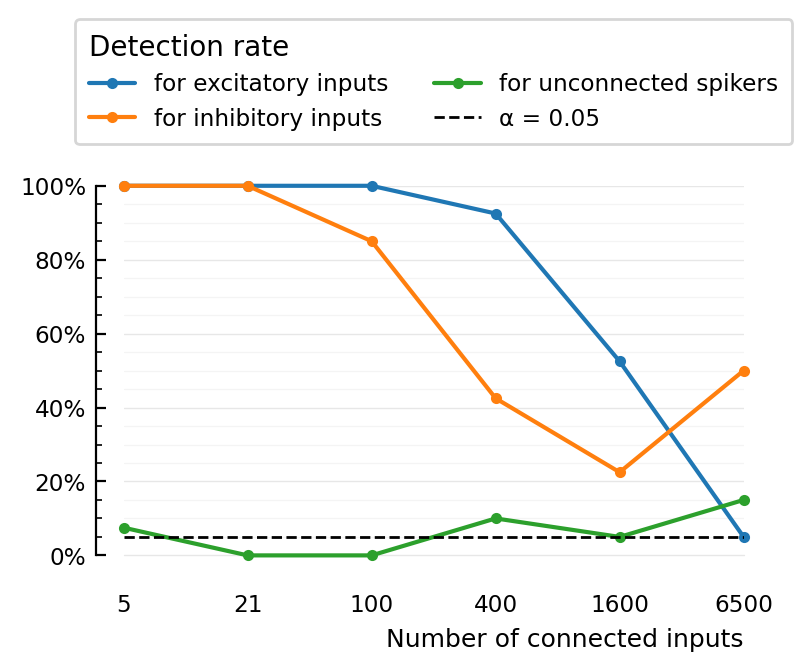
We see monotonic breakdown in excitatory connection detectability.
Same for inhibitory, except it’s not monotonic. Fluke due to sampling?
This plot must be improved with multiple simulations per condition rather than just single point.
(takes a while to run multiple 10’ N=6500 sims though).