2022-09-13 • Fit simpler model to STA – part 2
Contents
2022-09-13 • Fit simpler model to STA – part 2¶
Params¶
p = get_params(
duration = 10minutes,
p_conn = 0.04,
g_EE = 1,
g_EI = 1,
g_IE = 4,
g_II = 4,
ext_current = Normal(-0.5 * pA/√seconds, 5 * pA/√seconds),
E_inh = -80 * mV,
record_v = [1:40; 801:810],
);
Model function¶
linear_PSP(t; τ1, τ2) =
if (τ1 == τ2) @. t * exp(-t/τ1)
else @. τ1*τ2/(τ1-τ2) * (exp(-t/τ1) - exp(-t/τ2))
end;
gaussian(x; loc, width) =
@. exp(-0.5*( (x-loc)/width )^2);
# Note that unlike in the previous notebook, we do add the 1/2 factor in the exponent here
rescale_to_max!(x) =
x ./= maximum(abs.(x));
# Note that this returns `NaN`s if x .== 0
centre!(x) = (x .-= mean(x))
centre(x) = centre!(copy(x));
mult!(by) = x -> (x .*= by);
p0 = CVec(
tx_delay = 10ms,
bump = (
τ1 = 10ms,
τ2 = 12ms
),
dip = (
loc = 40ms,
width = 40ms,
weight = 0.15,
),
scale = 0mV,
);
FitParams = typeof(p0);
pbounds = CVec(
tx_delay = [0, 60ms],
bump = (
τ1 = [0, 100ms],
τ2 = [0, 100ms],
),
dip = (
loc = [20ms, 80ms],
width = [20ms, 80ms],
weight = [0, 0.6],
),
scale = [-2mV, 2mV],
)
pb_flat = collect(CVec(pbounds))
lower = pb_flat[1:2:end]
upper = pb_flat[2:2:end];
function model_STA_components(ep::ExpParams, fp::FitParams)
Δt::Float64 = ep.sim.general.Δt
STA_duration = ep.conntest.STA_window_length
@unpack tx_delay, bump, dip = fp
PSP_duration = STA_duration - tx_delay
delay_size = round(Int, tx_delay / Δt)
PSP_size = round(Int, PSP_duration / Δt)
STA_size = round(Int, STA_duration / Δt)
t_PSP = collect(linspace(0, PSP_duration, PSP_size))
t_STA = collect(linspace(0, STA_duration, STA_size))
add_delay(x) = vcat(zeros(Float64, delay_size), x)
# τ1, τ2 = bump
bump = (
linear_PSP(t_PSP; bump.τ1, bump.τ2)
|> rescale_to_max!
|> add_delay
)
# loc, width, weight = bump
dip = (
gaussian(t_STA; dip.loc, dip.width)
|> rescale_to_max!
|> mult!(-dip.weight)
)
return (; bump, dip)
end
function model_STA(ep::ExpParams, fp::FitParams)
bump, dip = model_STA_components(ep, fp)
STA = (
bump .+ dip
|> mult!(fp.scale)
|> centre!
)
end;
Fit¶
using LsqFit
# Code to adapt to LsqFit's API
p_buffer = copy(CVec(p0))
function toCVec(params::Vector, cv_buffer::CVec = p_buffer)
cv_buffer .= params
return cv_buffer
end
function fit_STA(STA, p0)
model(xdata, params) = model_STA(p, toCVec(params))
xdata = [] # Our model function generates
# xdata itself (it's alway the same).
ydata = centre(STA)
p0_vec = collect(CVec(p0))
fit = curve_fit(model, xdata, ydata, p0_vec; lower, upper)
end;
using PyPlot
using VoltoMapSim.Plot
function fit_STA(m::Int, p0 = p0, plot = true)
STA = calc_STA(m=>1, s, p)
fitt = fit_STA(STA, p0)
fp = toCVec(fitt.param)
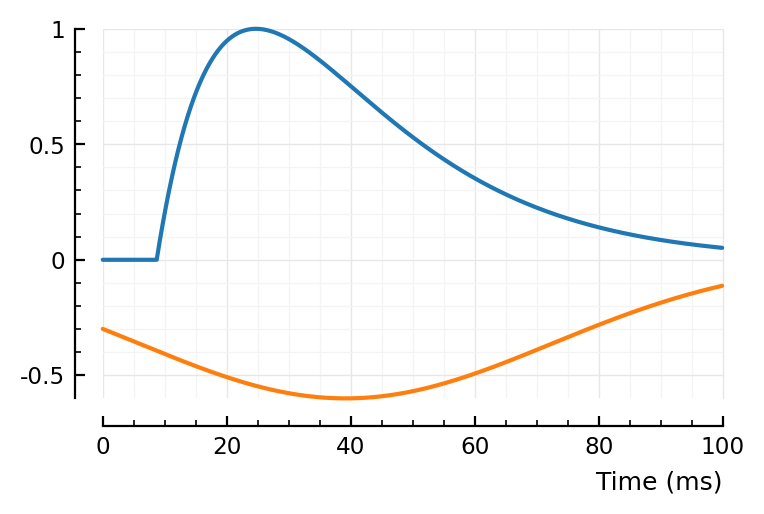
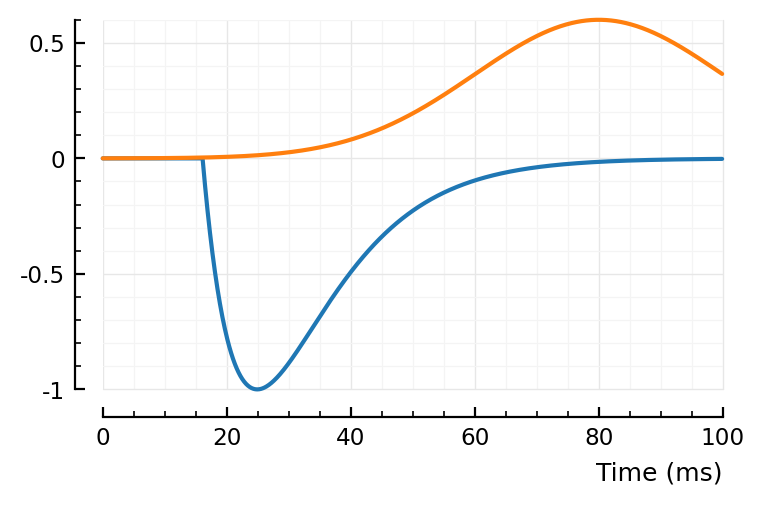
bump, dip = model_STA_components(p, fp)
sgn = sign(fp.scale)
plt.subplots()
plotsig(sgn * bump, p)
plotsig(sgn * dip, p)
plt.subplots()
plotsig(centre(STA) / mV, p, hylabel = "STA $m → 1")
plotsig(model_STA(p, fp) / mV, p)
println(NamedTuple(fp))
return fp
end;
fit_STA(894);
(tx_delay = 0.0101, bump = (τ1 = 0.0109, τ2 = 0.0111), dip = (loc = 0.0326, width = 0.0349, weight = 0.447), scale = -0.002)
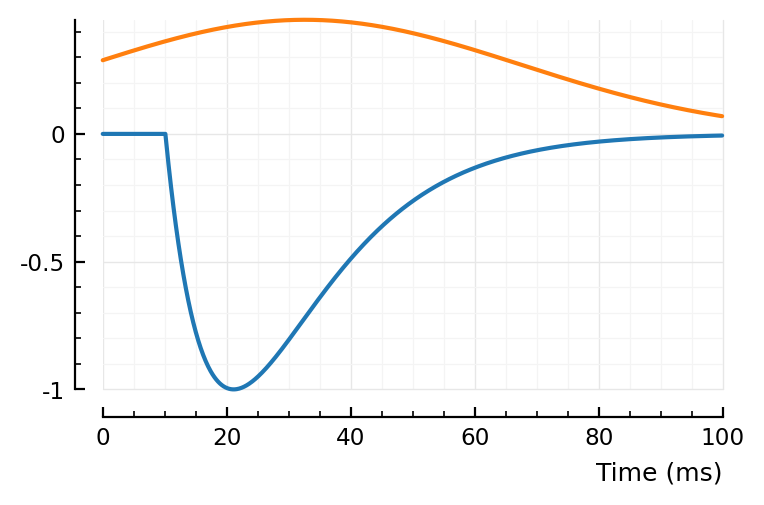
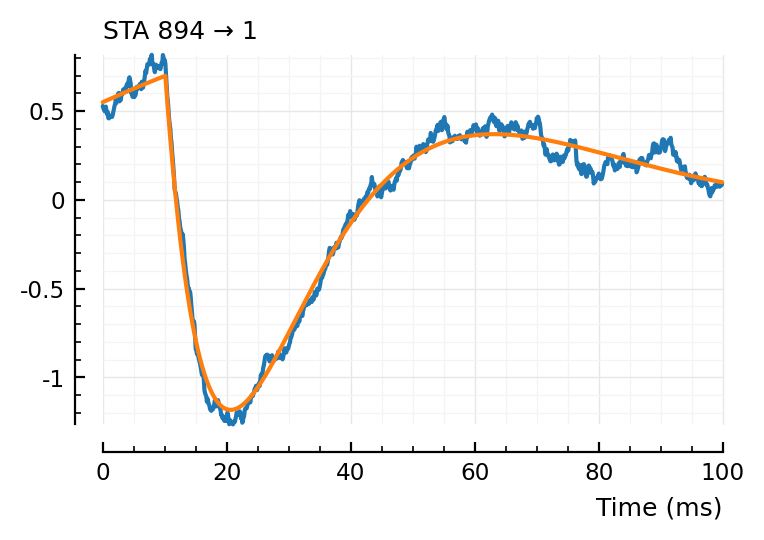
Aha! So it was the problem :D
Great. (Lesson: make parameters independent of each other).
Now to retry the STAs fitted two nb’s earlier.
Exc inputs¶
fit_STA.([139, 136, 132]);
(tx_delay = 0.0131, bump = (τ1 = 0.0131, τ2 = 0.0129), dip = (loc = 0.08, width = 0.08, weight = 0), scale = 0.000357)
(tx_delay = 0.0128, bump = (τ1 = 0.0112, τ2 = 0.0111), dip = (loc = 0.0508, width = 0.02, weight = 0.548), scale = 0.000371)
(tx_delay = 0.018, bump = (τ1 = 0.00883, τ2 = 0.0168), dip = (loc = 0.08, width = 0.02, weight = 0.122), scale = 0.000218)
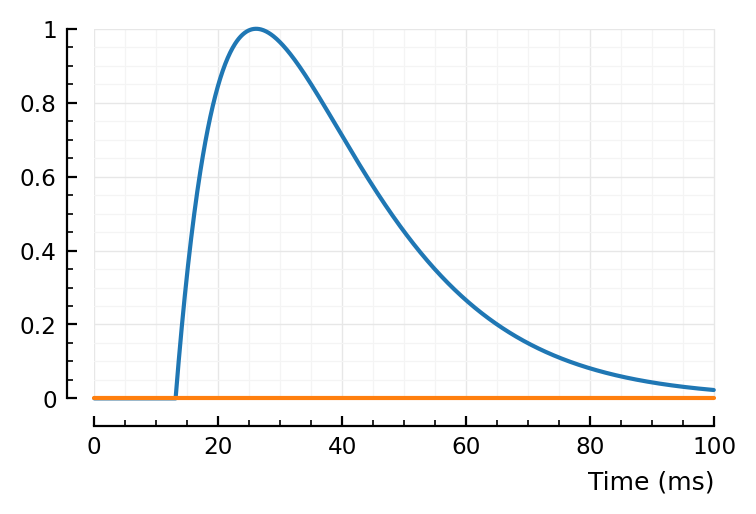
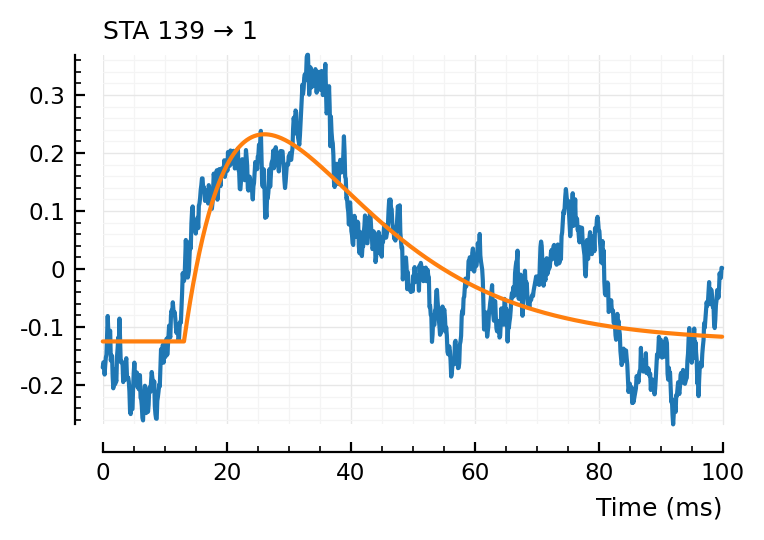
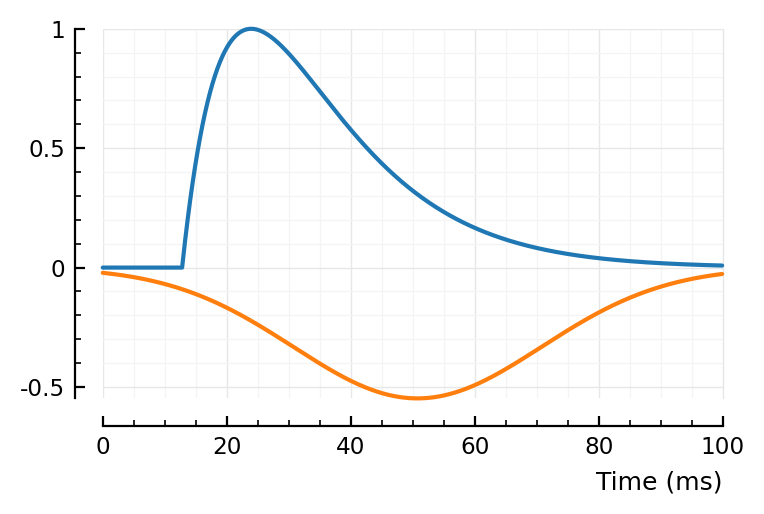
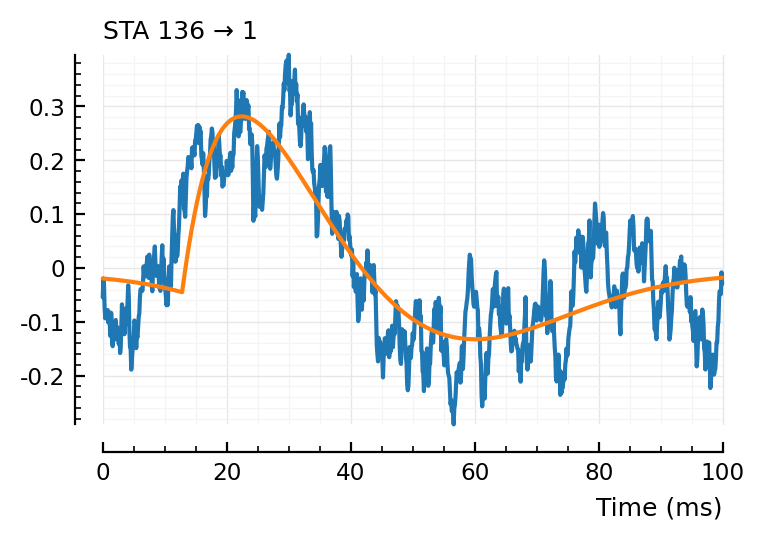
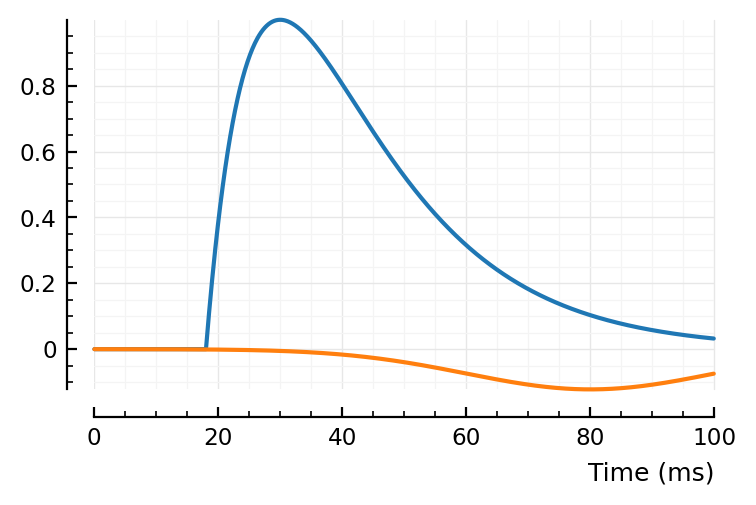
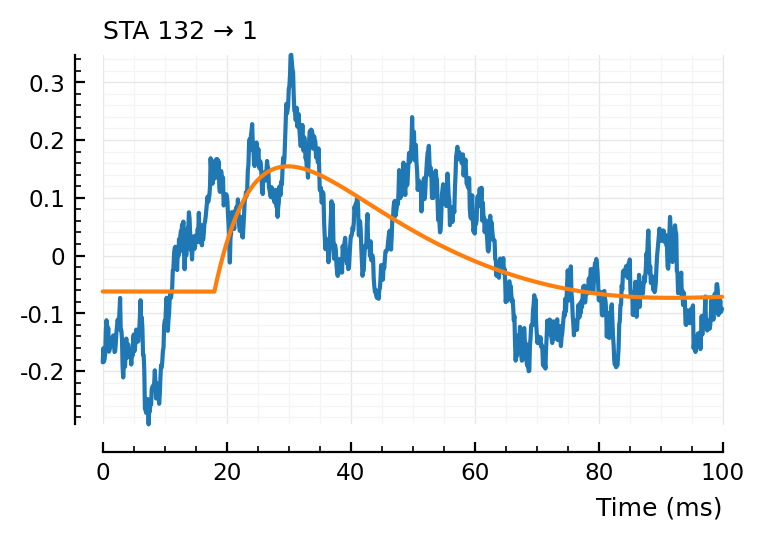
Excellent. No more wonky fits.
(The last one had ptp pval 0.03 btw. And avgSTA cor pval 0.12)
Inh inputs¶
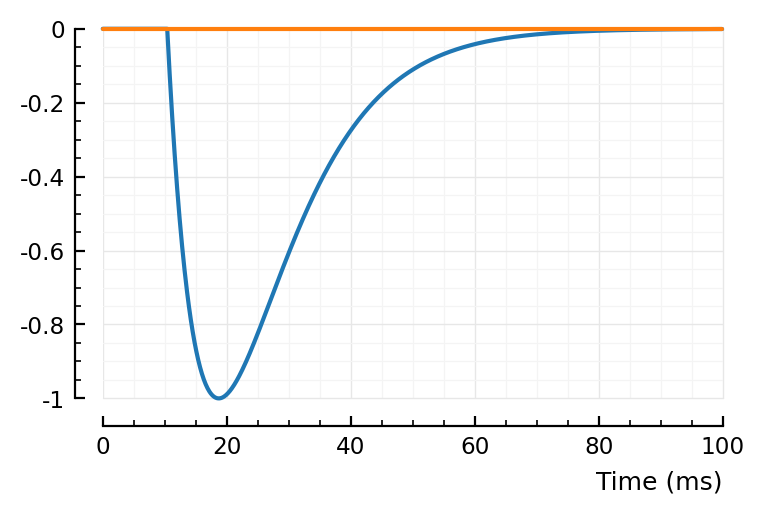
fit_STA.([988, 894, 831]);
(tx_delay = 0.0104, bump = (τ1 = 0.00822, τ2 = 0.00841), dip = (loc = 0.0739, width = 0.023, weight = 0), scale = -0.00039)
(tx_delay = 0.0101, bump = (τ1 = 0.0109, τ2 = 0.0111), dip = (loc = 0.0326, width = 0.0349, weight = 0.447), scale = -0.002)
(tx_delay = 0.0352, bump = (τ1 = 0.0164, τ2 = 0.000177), dip = (loc = 0.08, width = 0.02, weight = 1), scale = -0.000179)
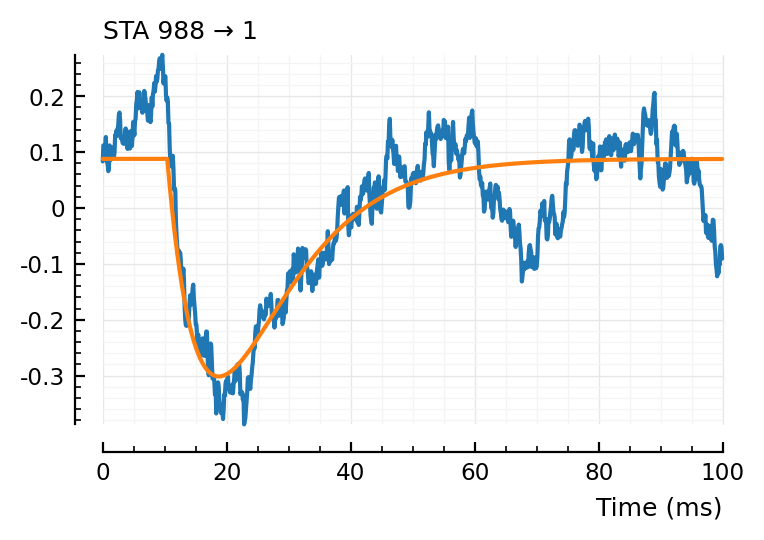
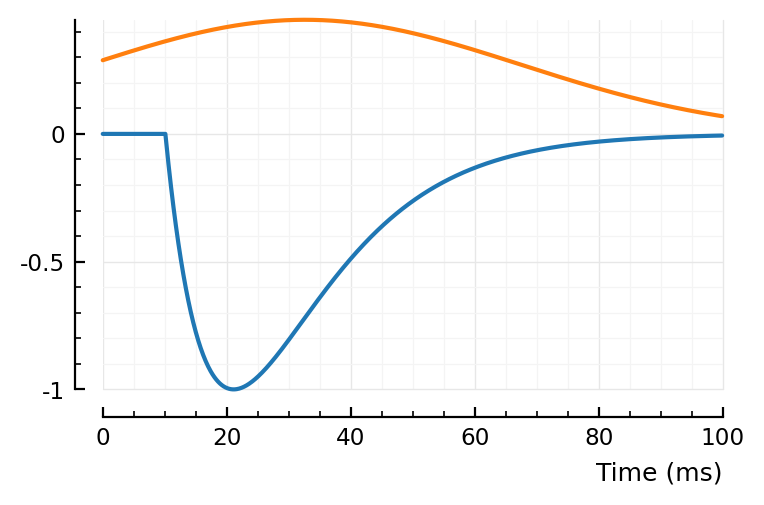
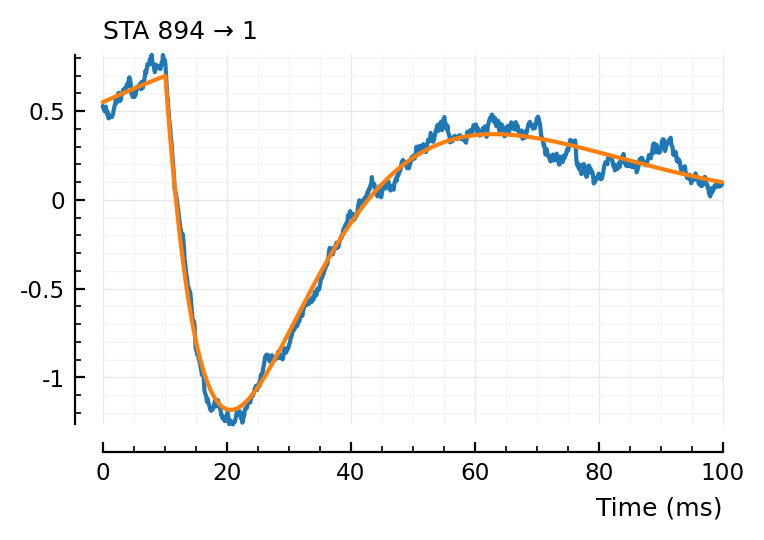
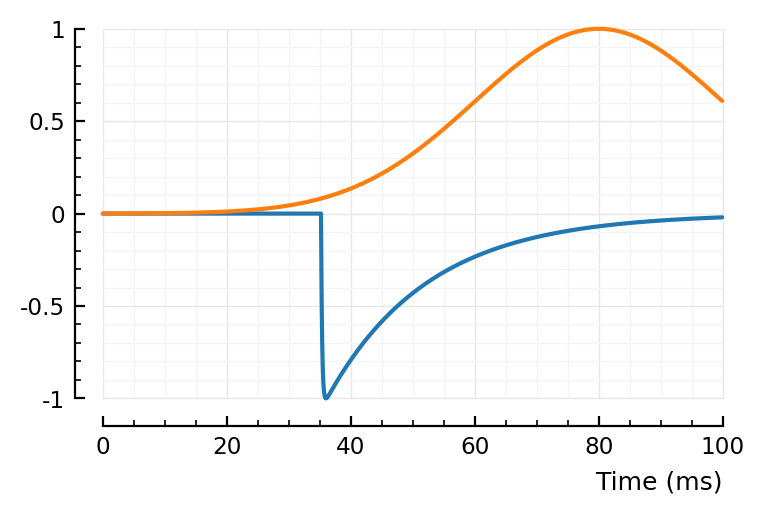
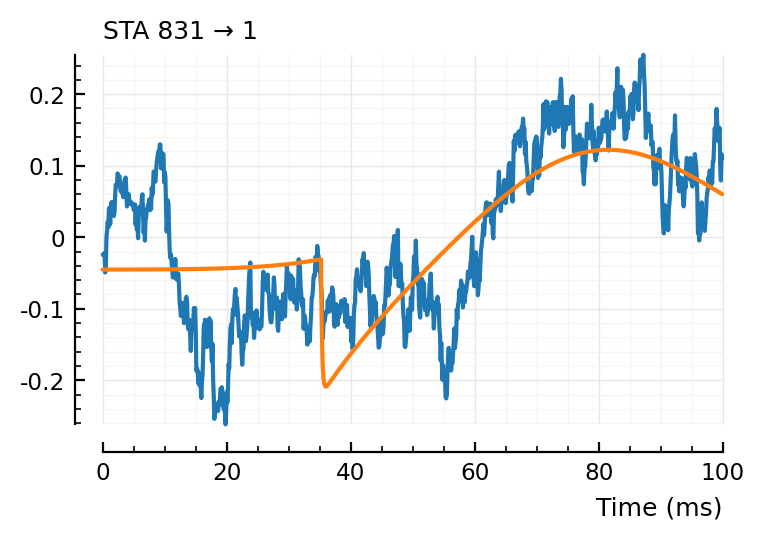
The first one could use the more important weighting around the bump.
The last one.. Well it’s the hardest inh input to detect.
We could do like a voting approach :P : “curve_fit thinks :non-input, ptp-area thinks :inh”.
After changing max dip.weight to 0.6:¶
(From 1)
fit_STA.([831]);
(tx_delay = 0.0147, bump = (τ1 = 0.0119, τ2 = 0.0124), dip = (loc = 0.08, width = 0.02, weight = 0.6), scale = -0.000177)
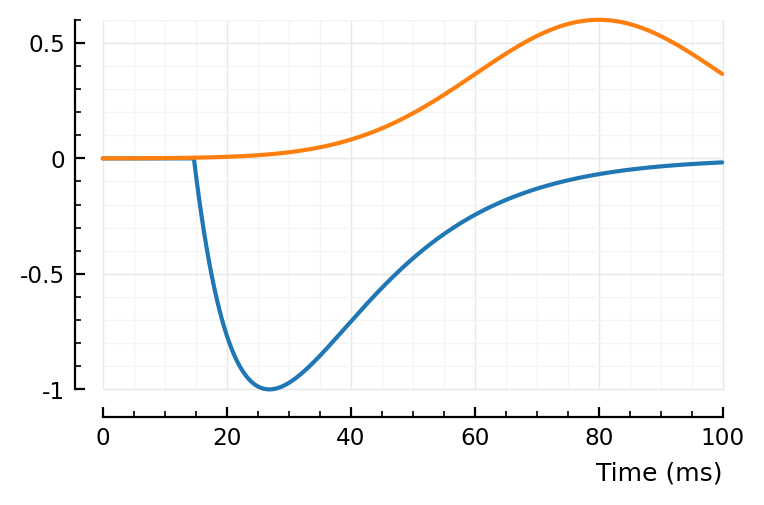
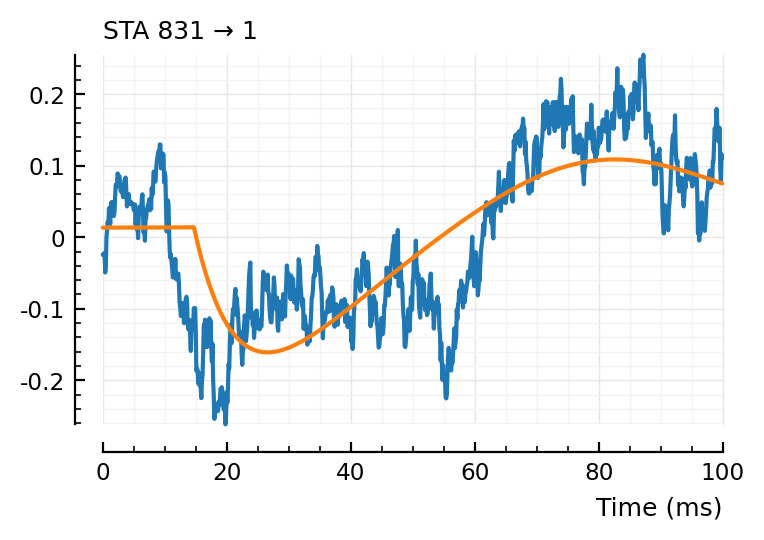
Great, much better.
Non-inputs¶
fit_STA.([23, 197, 367,332]);
(tx_delay = 1.01E-05, bump = (τ1 = 0.00248, τ2 = 0.00248), dip = (loc = 0.08, width = 0.02, weight = 0.453), scale = -0.000271)
(tx_delay = 0.00944, bump = (τ1 = 0.0254, τ2 = 0.0254), dip = (loc = 0.0507, width = 0.0288, weight = 1), scale = 0.000327)
(tx_delay = 0.0169, bump = (τ1 = 0.0123, τ2 = 0.00573), dip = (loc = 0.08, width = 0.02, weight = 0.973), scale = -0.000189)
(tx_delay = 0.0165, bump = (τ1 = 0.017, τ2 = 0.0169), dip = (loc = 0.0596, width = 0.0471, weight = 0.149), scale = -6.92E-06)
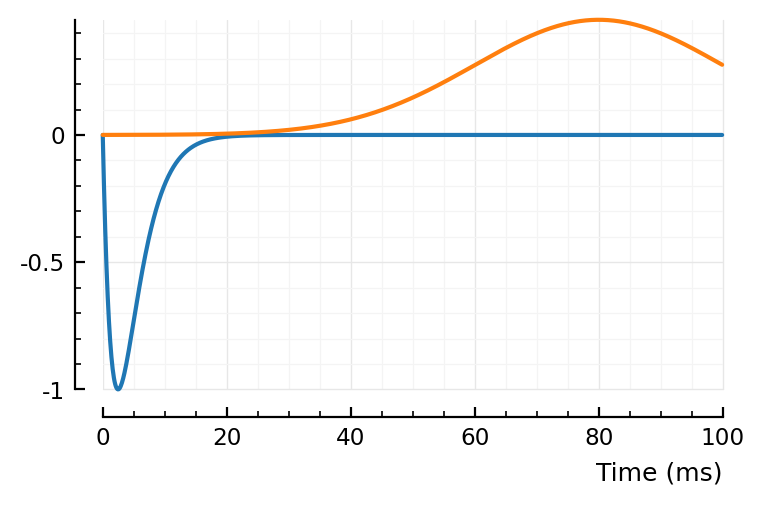
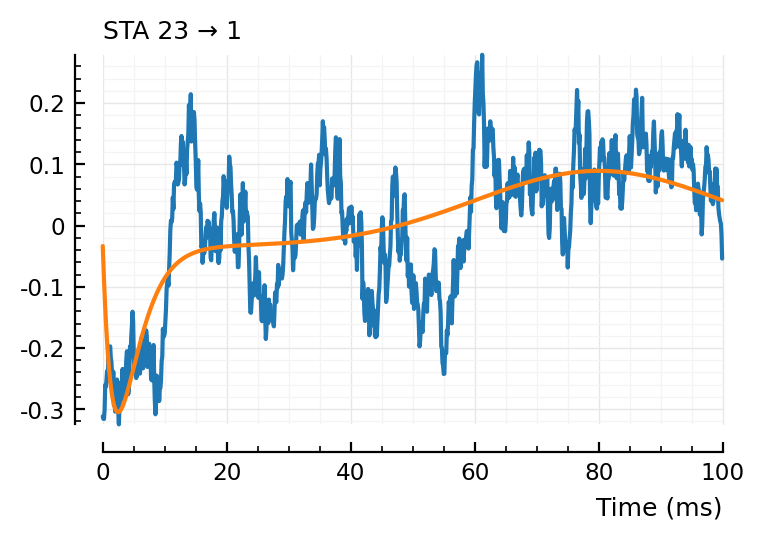
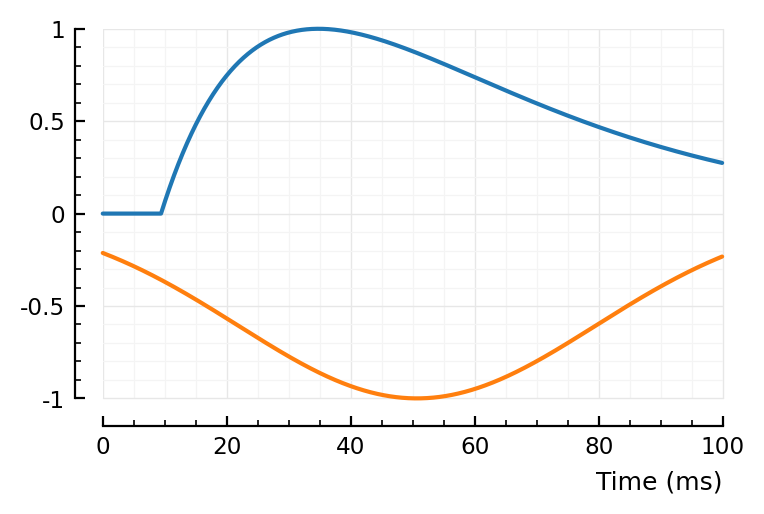
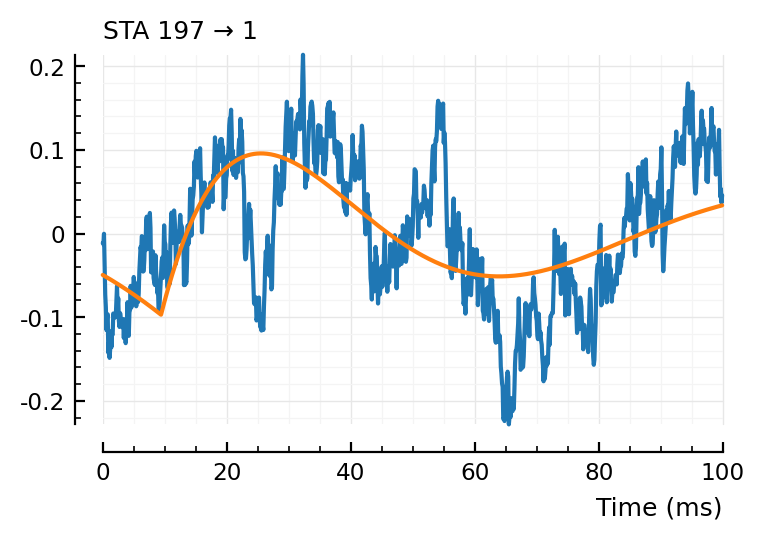
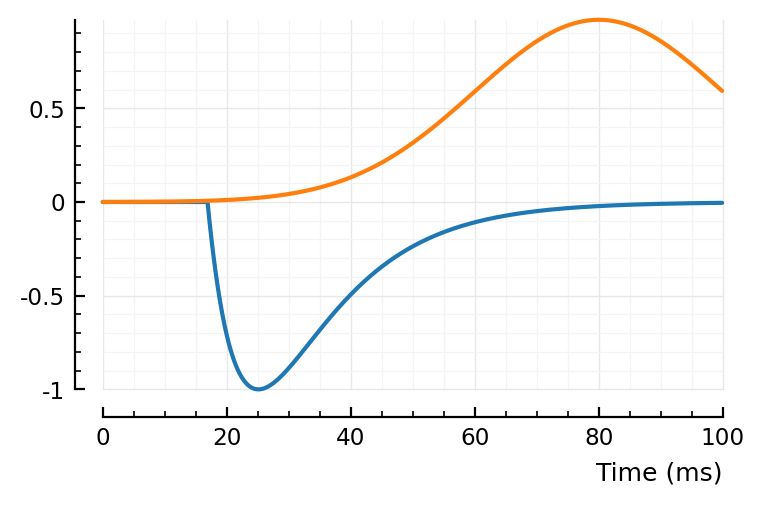
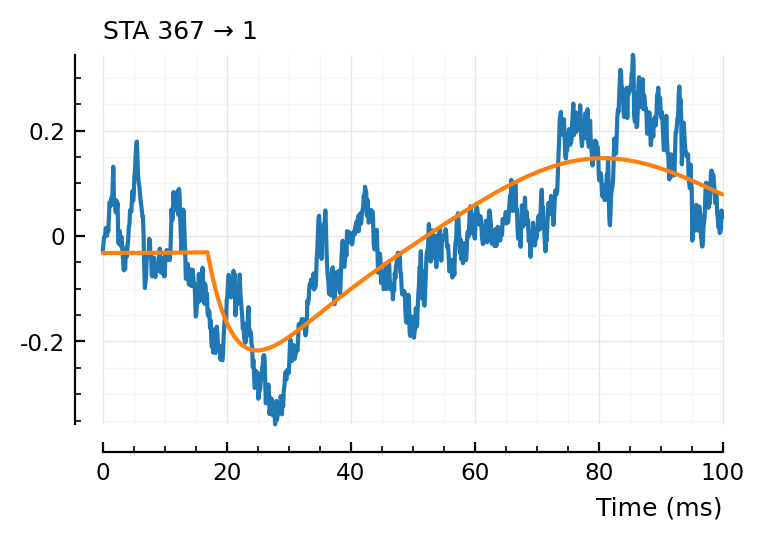
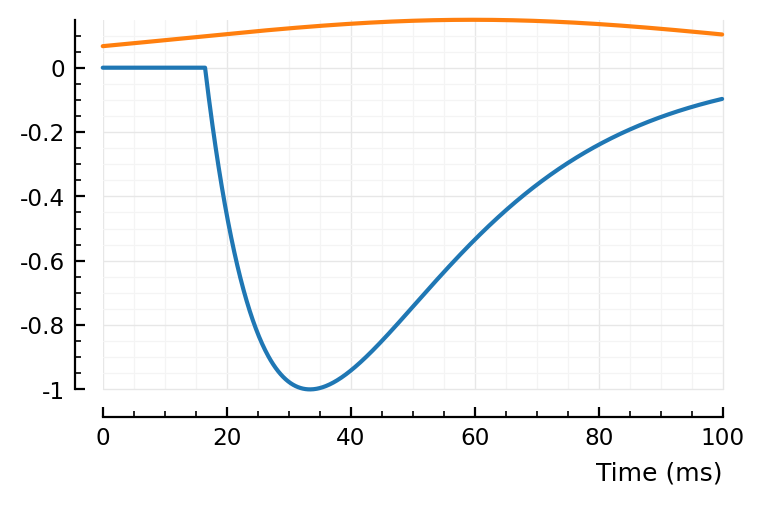
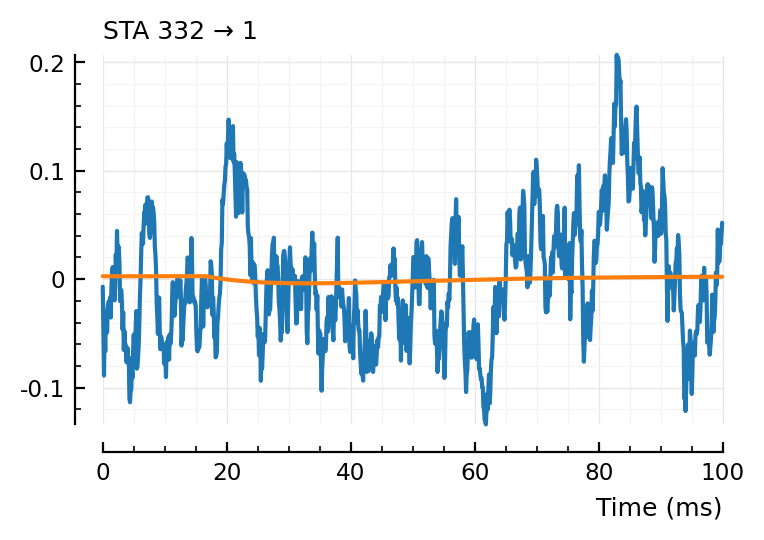
first and last (23, 332) good, nice and noisy
367 was a FP for the other two algo’s too.
197.. this one together with 367 and the last of the inh’s above makes me think the max weight of the bump is too high.
and again, that we should weight around the bump more somehow.
After changing max dip.weight to 0.6:¶
(Middle two)
fit_STA.([197, 367]);
(tx_delay = 0.00866, bump = (τ1 = 0.016, τ2 = 0.016), dip = (loc = 0.0392, width = 0.0332, weight = 0.6), scale = 0.000186)
(tx_delay = 0.0161, bump = (τ1 = 0.00975, τ2 = 0.00799), dip = (loc = 0.08, width = 0.02, weight = 0.6), scale = -0.000234)
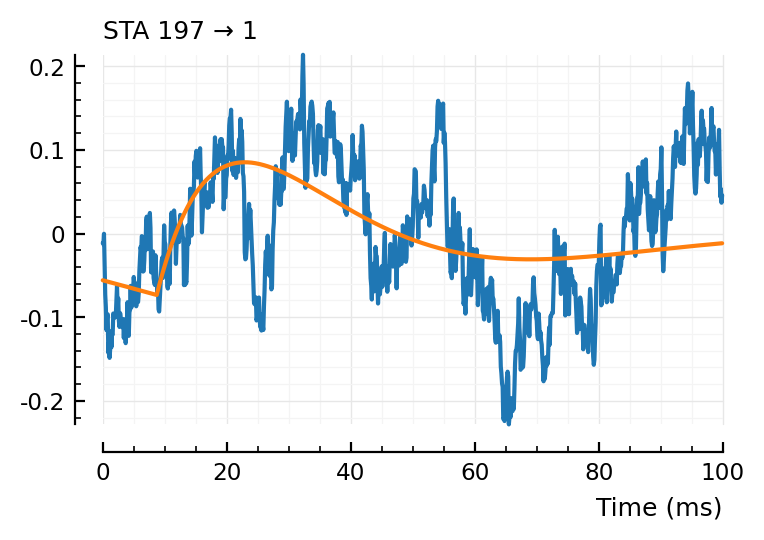
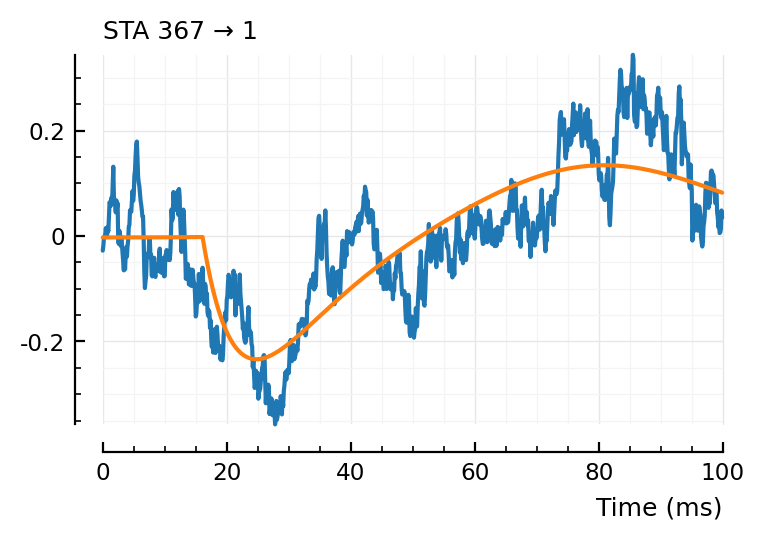
Nice, the 197 is much less well fit now.