2022-09-09 • Connection test using template matching¶

Imports¶

using Revise

using MyToolbox

using VoltoMapSim

Params¶

p = get_params(
    duration = 10minutes,
    p_conn = 0.04,
    g_EE = 1,
    g_EI = 1,
    g_IE = 4,
    g_II = 4,
    ext_current = Normal(-0.5 * pA/√seconds, 5 * pA/√seconds),
    E_inh = -80 * mV,
    record_v = [1:40; 801:810],
);

Run sim¶

s = cached(sim, [p.sim]);

s = augment_simdata(s, p);

Peak-to-peak perf¶

perf = cached_conntest_eval(s, 1, p)
perf.detection_rates

(TPR_exc = 0.615, TPR_inh = 0.9, FPR = 0.125)

(this is just for one postsyn neuron. For all 40 recorded, see here)

Can we get TPR_exc up?

Idea is to use a template STA to correlate STA with. Here we’ll cheat and use the average (E→E) STA as template (cheating cause it presumes knowledge of what’s connected). This is to test viability. If this works, we can move on to fitting a parametrized analytical STA shape to an individual STA (and then somehow compare it to shuffles..).

Template: average STA¶

using PyPlot
using VoltoMapSim.Plot

exc_post = [1:40;]
avgSTA = nothing
N = 0
@showprogress for n in exc_post
    ii = s.input_info[n]
    for m in ii.exc_inputs
        STA = calc_STA(m, n, s,p)
        if isnothing(avgSTA) avgSTA = STA
        else avgSTA .+= STA end
        N += 1
    end
end
avgSTA ./= N

plotsig(avgSTA / mV, p);

Progress: 100%|█████████████████████████████████████████| Time: 0:00:1239m39m

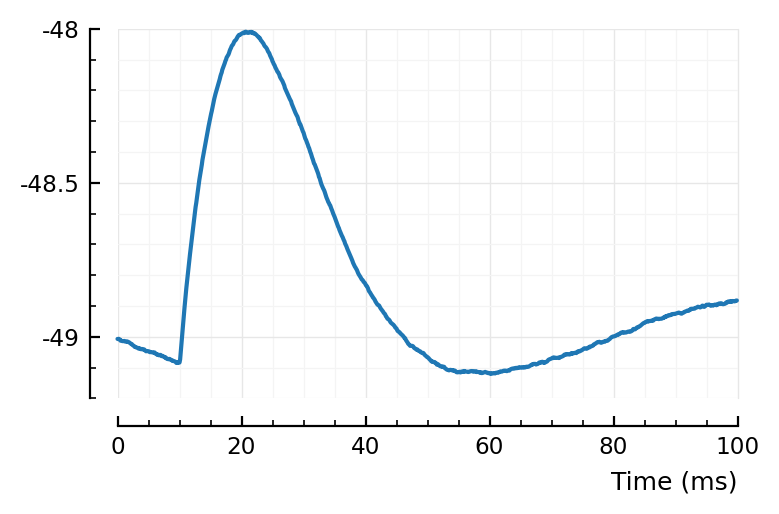
../_images/2022-09-09__Conntest_with_template_matching_17_1.png

Great. Now we’ll use this for conntest.

We’ll take one difficult connection as example. (See previous notebook)

m = 136
n = 1
plotSTA(m, n, s,p);

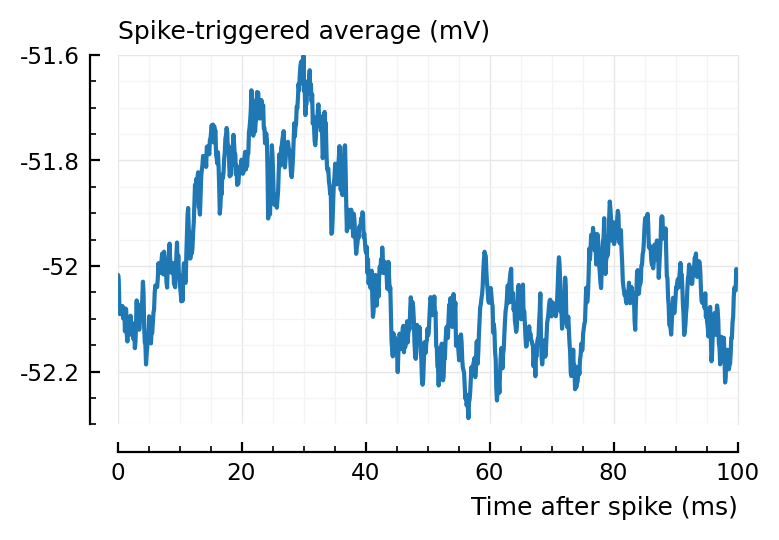
../_images/2022-09-09__Conntest_with_template_matching_19_0.png

Pval of 136 was 0.09.

STA = calc_STA(m,n,s,p);

ref_to_start(sig) = sig .- sig[1]
fig,ax = plt.subplots()
plotsig(ref_to_start(avgSTA) / mV, p; ax)
plotsig(ref_to_start(STA) / mV, p; ax)
add_refline(ax);

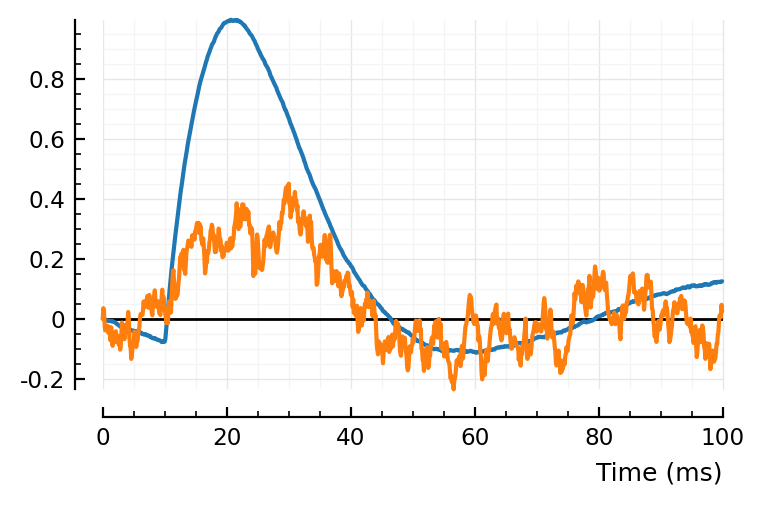
../_images/2022-09-09__Conntest_with_template_matching_22_0.png

And what if we ref to mean? (Which is what’d happen if we’d calculate (Pearson) correlation between signal and template).

centre(sig) = sig .- mean(sig)
fig,ax = plt.subplots()
plotsig(centre(avgSTA) / mV, p; ax)
plotsig(centre(STA) / mV, p; ax)
add_refline(ax);

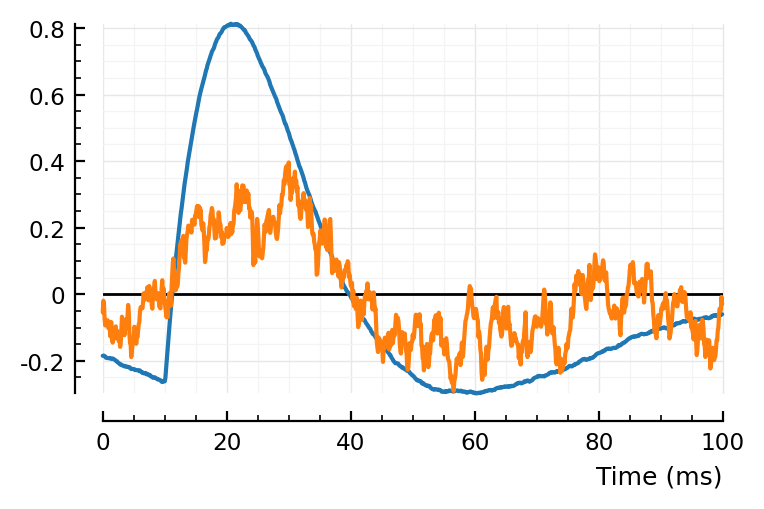
../_images/2022-09-09__Conntest_with_template_matching_24_0.png

I like the former better, signals seem aligned better.

Though otoh, the first sample is more noisy than the mean of all samples of the STA.

Alright let’s go for mean centring.

corr = cor(STA, avgSTA)

0.84

Correlate shuffleds w/ template¶

Now do the same for shuffled STAs.

spikes = s.spike_times[m]
v = s.signals[n].v
shuffled_corrs = Float64[]
for i in 1:100
    shuffled_STA = calc_STA(v, shuffle_ISIs(spikes), p)
    push!(shuffled_corrs, cor(template, shuffled_STA))
end

ydistplot(shuffled_corrs, ref = corr, ylim = [-1,1]);

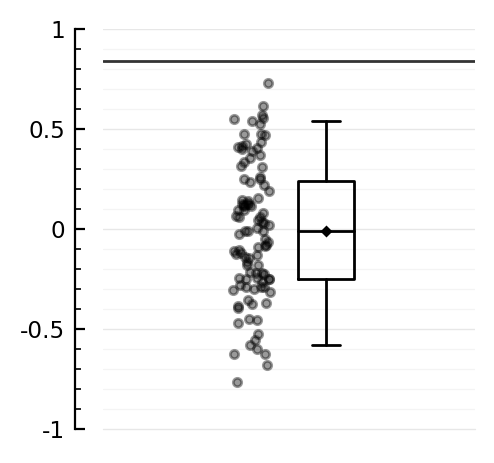
../_images/2022-09-09__Conntest_with_template_matching_31_0.png

Aha, so for this one we beat the p = 0.09 :)
(with p < 0.01)

Use as conntest, for all exc inputs¶

We went to apply to all 1’s exc inputs now.

First, reuse our test_connection function in the codebase
(we add an argument f to pass an arbitrary test statistic function).

test_statistic(STA) = cor(STA, avgSTA)

pval = test_connection(v, spikes, p, test_statistic)

0.01

Good, same as above.

ii = s.input_info[n]
corrs = Float64[]
pvals = Float64[]
@showprogress for m in ii.exc_inputs
    push!(pvals, test_connection(v, s.spike_times[m], p, test_statistic))
    push!(corrs, cor(calc_STA(m,n,s,p), avgSTA))
end;

Progress: 100%|█████████████████████████████████████████| Time: 0:00:26

ENV["COLUMNS"] = 100;

tn = perf.tested_neurons
df = tn[tn.real_type .== :exc, :]
df.pval_with_template_corr = pvals
df.corr_with_template = corrs
df

26 rows × 7 columns

	input_neuron_ID	real_type	predicted_type	pval	area_over_start	pval_with_template_corr	corr_with_template
	Int64	Symbol	Symbol	Float64	Float64	Float64	Float64
1	139	exc	exc	0.01	17	0.01	0.639
2	681	exc	inh	0.01	-4	0.01	0.814
3	11	exc	exc	0.01	18	0.01	0.844
4	766	exc	exc	0.01	52	0.01	0.939
5	132	exc	exc	0.03	18.5	0.12	0.504
6	516	exc	exc	0.01	30.4	0.01	0.95
7	418	exc	inh	0.01	-3.7	0.01	0.935
8	565	exc	unconn	0.05	18.7	0.01	0.735
9	597	exc	exc	0.01	26.3	0.01	0.956
10	446	exc	exc	0.01	19.4	0.01	0.876
11	447	exc	exc	0.01	40.3	0.01	0.881
12	710	exc	exc	0.01	28.6	0.01	0.929
13	66	exc	exc	0.01	8.29	0.01	0.899
14	136	exc	unconn	0.09	5.45	0.01	0.84
15	312	exc	exc	0.01	82.6	0.01	0.948
16	145	exc	inh	0.01	-27.8	0.01	0.793
17	169	exc	exc	0.01	50.6	0.01	0.928
18	194	exc	unconn	0.35	-1.99	0.01	0.689
19	629	exc	exc	0.01	4.7	0.01	0.679
20	352	exc	unconn	0.82	-8.92	0.03	0.441
21	800	exc	unconn	0.72	-4.17	0.01	0.707
22	303	exc	exc	0.01	2.51	0.01	0.9
23	101	exc	unconn	0.29	21.1	0.19	0.37
24	70	exc	exc	0.01	16.9	0.01	0.958
25	337	exc	exc	0.01	12	0.04	0.592
26	33	exc	unconn	0.18	10.6	0.35	0.102

Changes wrt previous statistic (peak-to-peak):

565, 136, 194, 352, 800 correctly detected now
101 and 33 still not detected (see prev nb for STA plots).
132 not detected anymore (and 337’s p value went up to 0.04)

plotSTA(132, 1, s,p);
plotSTA(337, 1, s,p);

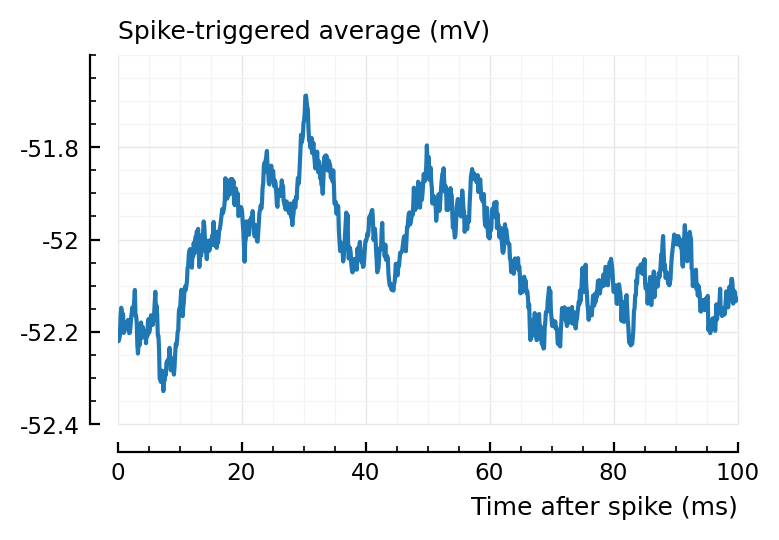
../_images/2022-09-09__Conntest_with_template_matching_42_0.png

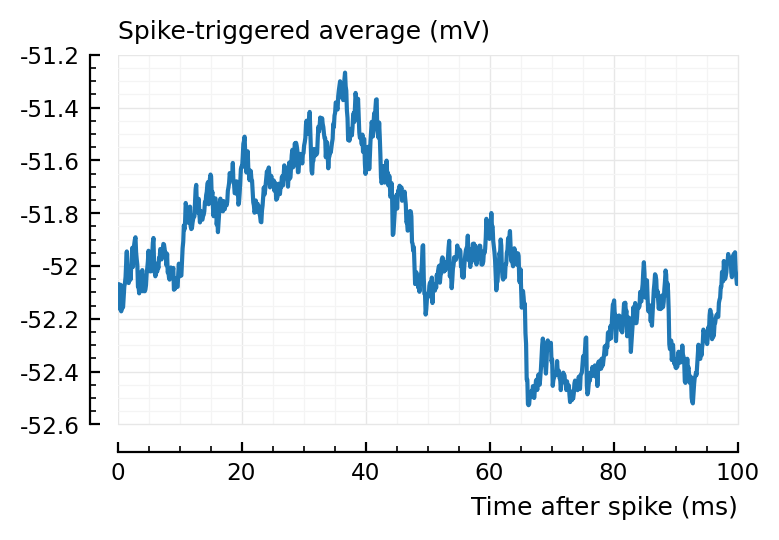
../_images/2022-09-09__Conntest_with_template_matching_42_1.png

Ignoring the predicted type == inh for now (which is a different problem – though we might solve by using corr instead of area over start) ..

df = df[df.predicted_type .!= :inh, :]
# TPR_exc_ptp = 
TPR_exc_ptp = count(df.pval .< 0.05) / nrow(df)

0.696

TPR_exc_template_match = count(df.pval_with_template_corr .< 0.05) / nrow(df)

0.87

That seems like an improvement.

Same but for inh inputs¶

test_statistic(STA) = -cor(STA, avgSTA);

Here we use the negative corr as test stat.

This will require determining the type of a potential connection first, before deciding whether it exists.

corrs = Float64[]
pvals = Float64[]
@showprogress for m in ii.inh_inputs
    push!(pvals, test_connection(v, s.spike_times[m], p, test_statistic))
    push!(corrs, cor(calc_STA(m,n,s,p), avgSTA))
end;

Progress: 100%|█████████████████████████████████████████| Time: 0:00:10

df = tn[tn.real_type .== :inh, :]
df.pval_with_template_corr = pvals
df.corrs_with_template = corrs
df

10 rows × 7 columns

	input_neuron_ID	real_type	predicted_type	pval	area_over_start	pval_with_template_corr	corrs_with_template
	Int64	Symbol	Symbol	Float64	Float64	Float64	Float64
1	988	inh	inh	0.01	-8.34	0.01	-0.865
2	894	inh	inh	0.01	-52.9	0.01	-0.966
3	831	inh	exc	0.03	2.46	0.03	-0.563
4	902	inh	inh	0.01	-59.7	0.01	-0.977
5	897	inh	inh	0.01	-59.3	0.01	-0.979
6	928	inh	inh	0.01	-62.6	0.01	-0.97
7	914	inh	inh	0.01	-27	0.01	-0.972
8	829	inh	inh	0.01	-17.2	0.01	-0.932
9	908	inh	inh	0.01	-89.6	0.01	-0.873
10	922	inh	inh	0.01	-45.9	0.01	-0.784

Aha, the correlations are all negative.
And they were all positive for the exc inputs. So this is a better exc-or-inh decider.

And same performance, voila :)

Now for unconnected inputs.¶

df = tn[tn.real_type .== :unconn, :];

corrs = Float64[]
pvals = Float64[]
predtypes = Symbol[]
@showprogress for m in df.input_neuron_ID
    corr = cor(calc_STA(m,n,s,p), avgSTA)
    if (corr > 0) test_statistic(STA) = cor(STA, avgSTA)
    else          test_statistic(STA) = -cor(STA, avgSTA) end
    pval = test_connection(v, s.spike_times[m], p, test_statistic)
    if (pval ≥ 0.05)     predtype = :unconn
    elseif (corr > 0)    predtype = :exc
    else                 predtype = :inh end
    push!(pvals, pval)
    push!(corrs, corr)
    push!(predtypes, predtype)
end;

Progress: 100%|█████████████████████████████████████████| Time: 0:00:41

ENV["LINES"] = 100;
ENV["COLUMNS"] = 200;

df.predtype_corr = predtypes
df.pval_with_template_corr = pvals
df.corrs_with_template = corrs
df

40 rows × 8 columns

	input_neuron_ID	real_type	predicted_type	pval	area_over_start	predtype_corr	pval_with_template_corr	corrs_with_template
	Int64	Symbol	Symbol	Float64	Float64	Symbol	Float64	Float64
1	23	unconn	unconn	0.42	31.2	unconn	0.51	0.0247
2	25	unconn	unconn	0.6	-13.3	unconn	0.21	-0.203
3	86	unconn	unconn	0.33	-11.2	unconn	0.32	0.121
4	113	unconn	unconn	0.64	-11	unconn	0.17	-0.385
5	197	unconn	unconn	0.65	1.15	unconn	0.1	0.416
6	227	unconn	unconn	0.95	9.94	unconn	0.2	0.336
7	230	unconn	unconn	0.39	7.05	unconn	0.2	-0.281
8	262	unconn	unconn	0.07	9.06	unconn	0.39	-0.0677
9	269	unconn	unconn	0.45	6.56	unconn	0.27	0.195
10	323	unconn	unconn	0.4	3.37	unconn	0.22	0.317
11	332	unconn	unconn	0.88	0.694	unconn	0.42	0.0811
12	367	unconn	exc	0.02	2.77	inh	0.01	-0.613
13	394	unconn	unconn	1	-6.72	unconn	0.12	0.391
14	410	unconn	unconn	0.7	3.76	unconn	0.24	0.145
15	424	unconn	unconn	0.22	21.4	unconn	0.29	0.119
16	439	unconn	unconn	0.08	-57.6	unconn	0.2	0.319
17	460	unconn	unconn	0.08	21.5	exc	0.04	0.591
18	487	unconn	unconn	0.32	-7.35	unconn	0.42	-0.0949
19	499	unconn	exc	0.01	2.17	inh	0.02	-0.638
20	521	unconn	unconn	0.37	5.41	unconn	0.38	0.0533
21	537	unconn	unconn	0.22	-2.49	unconn	0.12	0.381
22	547	unconn	inh	0.04	-18.2	unconn	0.43	-0.097
23	599	unconn	unconn	0.15	-10.6	exc	0.03	0.634
24	612	unconn	inh	0.01	-34.3	unconn	0.56	0.0091
25	646	unconn	unconn	0.39	-1.08	unconn	0.44	0.0809
26	669	unconn	unconn	0.27	-20	unconn	0.21	0.262
27	702	unconn	unconn	0.49	-21	unconn	0.45	-0.0646
28	722	unconn	unconn	0.52	-5.28	unconn	0.26	-0.217
29	768	unconn	unconn	0.33	22.8	inh	0.02	-0.613
30	790	unconn	unconn	0.58	-0.542	inh	0.03	-0.52
31	813	unconn	unconn	0.46	-23.2	unconn	0.07	0.488
32	821	unconn	unconn	0.5	-3.52	unconn	0.14	-0.357
33	842	unconn	unconn	0.08	6.56	unconn	0.11	-0.417
34	843	unconn	unconn	0.27	10.1	unconn	0.14	-0.333
35	875	unconn	unconn	0.49	-47.3	unconn	0.21	-0.339
36	882	unconn	unconn	0.16	-5.13	exc	0.04	0.53
37	896	unconn	unconn	0.86	-20.6	unconn	0.35	-0.0805
38	921	unconn	unconn	0.88	-3.81	unconn	0.11	0.433
39	956	unconn	unconn	0.7	-10.5	unconn	0.11	0.396
40	977	unconn	exc	0.04	21.7	unconn	0.39	-0.091

WARNING: both Plot and PyPlot export "plot"; uses of it in module Main must be qualified

FPR__ptp = count(df.pval .< 0.05) / nrow(df)

0.125

FPR__template_match = count(df.pval_with_template_corr .< 0.05) / nrow(df)

0.125

So no change in the FPR (at α 0.05 at least).

Plot the interesting cases where predictions differ.

function plotcase(m)
    row = first(df[df.input_neuron_ID .== m, :])
    title = jn("ptp:  $(row.predicted_type) ($(row.pval))",
               "corr: $(row.predtype_corr) ($(row.pval_with_template_corr))")
    plotSTA(m,n,s,p, hylabel="STA $m (unconn) → $n"; title)
end
for m in df[(df.predicted_type .!= :unconn) .| (df.predtype_corr .!= :unconn), :].input_neuron_ID
    plotcase(m)
end

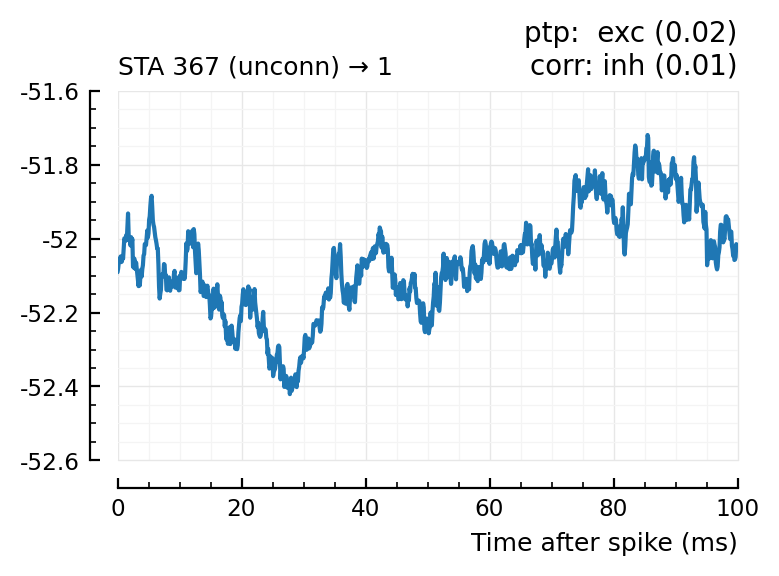
../_images/2022-09-09__Conntest_with_template_matching_63_0.png

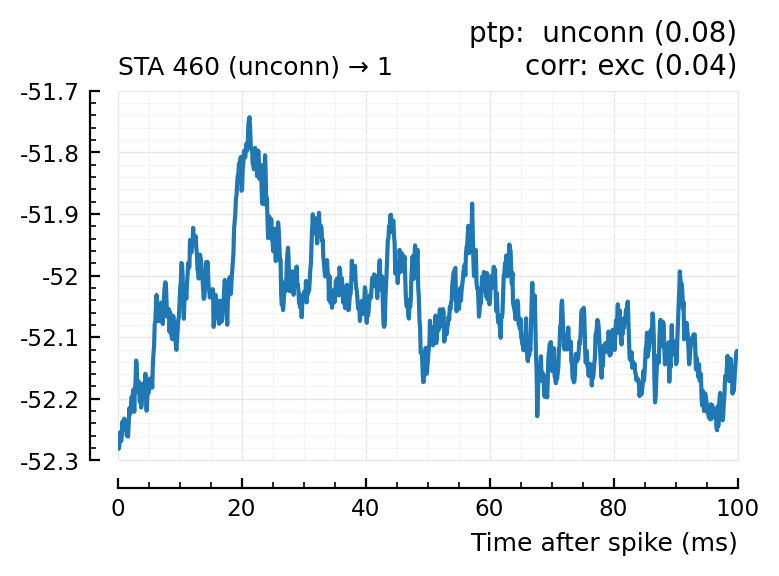
../_images/2022-09-09__Conntest_with_template_matching_63_1.png

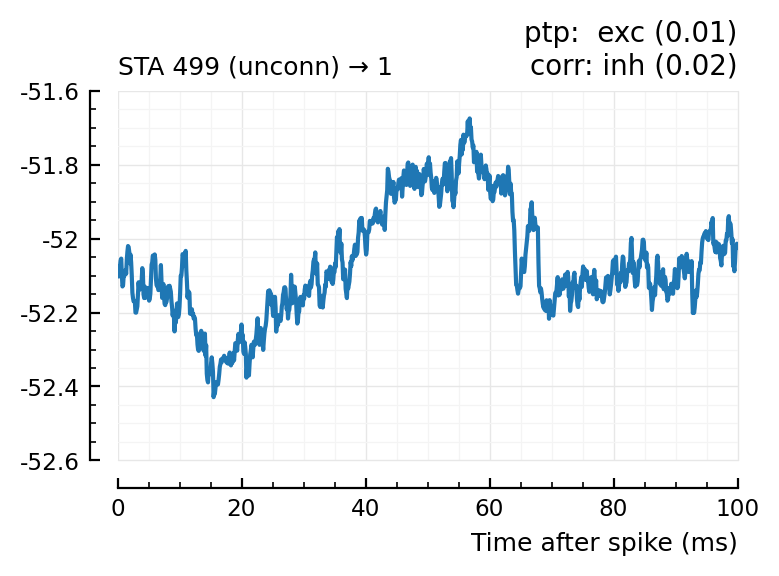
../_images/2022-09-09__Conntest_with_template_matching_63_2.png

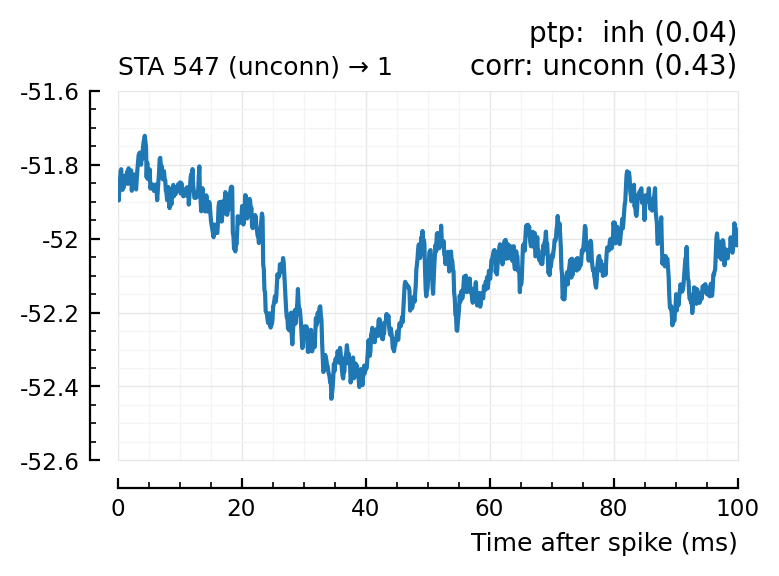
../_images/2022-09-09__Conntest_with_template_matching_63_3.png

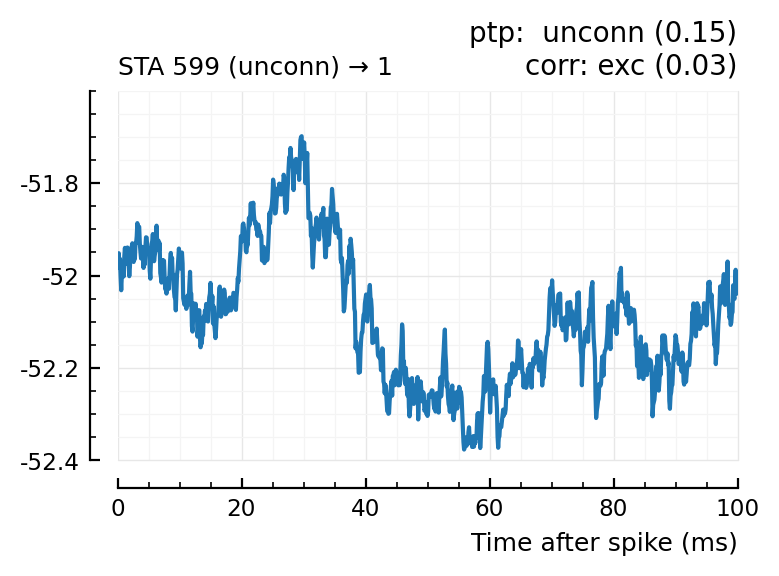
../_images/2022-09-09__Conntest_with_template_matching_63_4.png

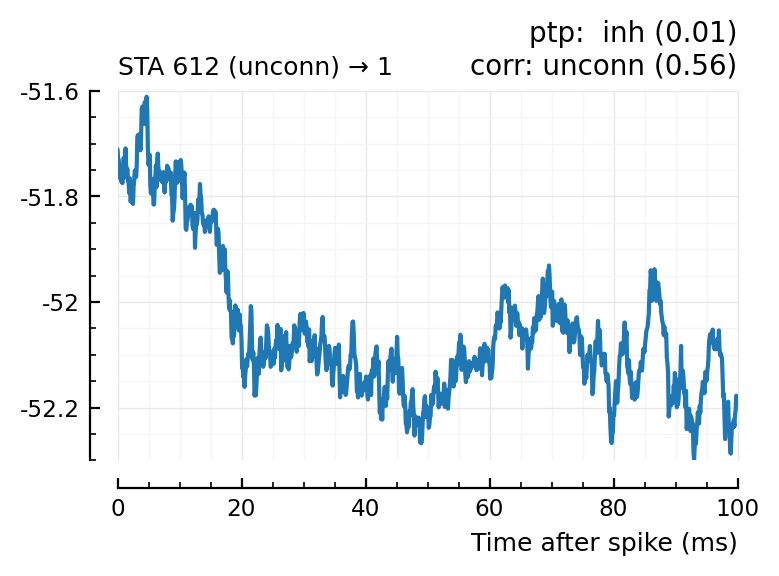
../_images/2022-09-09__Conntest_with_template_matching_63_5.png

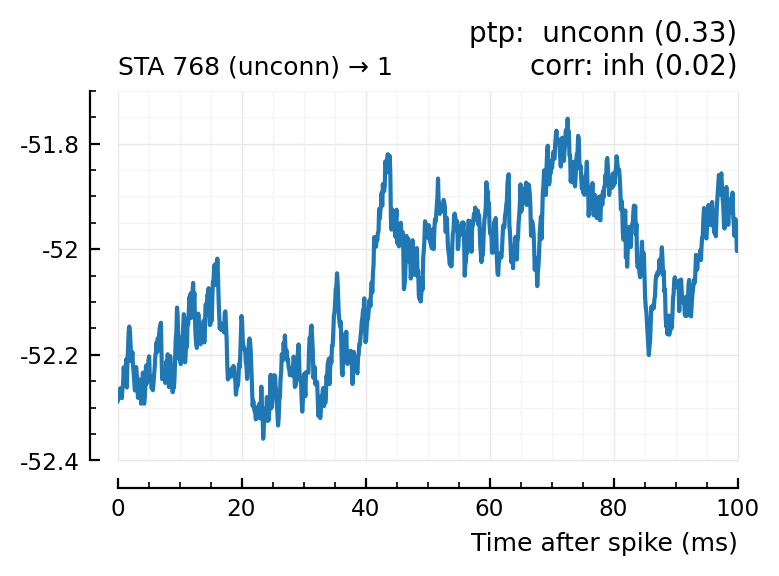
../_images/2022-09-09__Conntest_with_template_matching_63_6.png

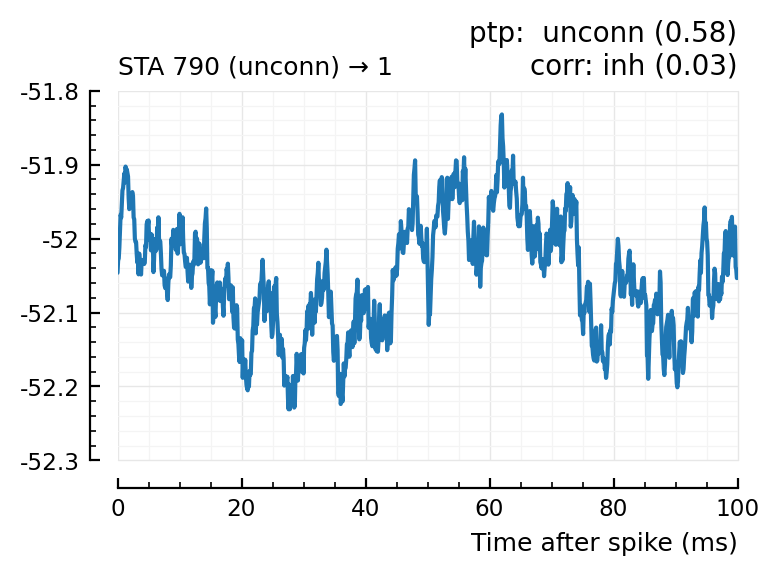
../_images/2022-09-09__Conntest_with_template_matching_63_7.png

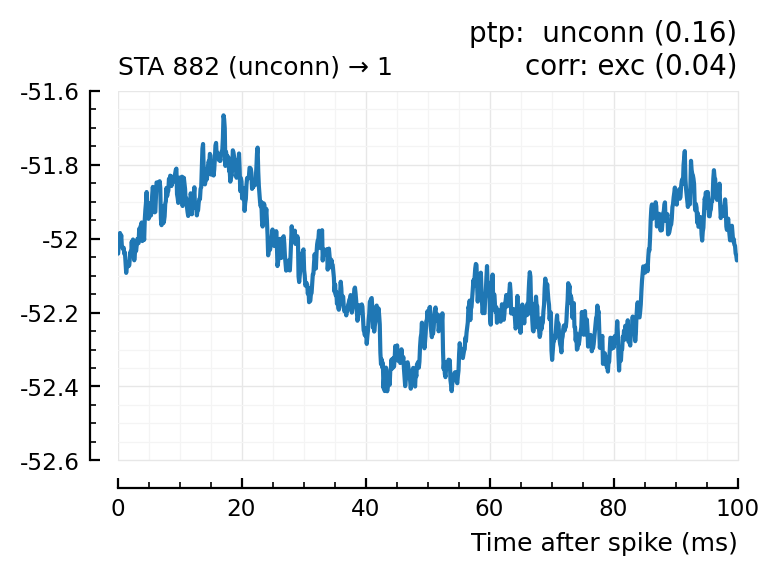
../_images/2022-09-09__Conntest_with_template_matching_63_8.png

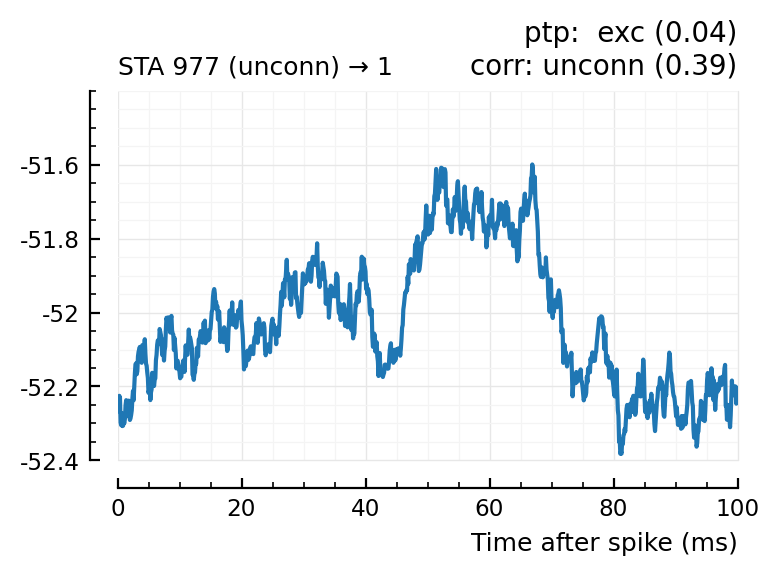
../_images/2022-09-09__Conntest_with_template_matching_63_9.png

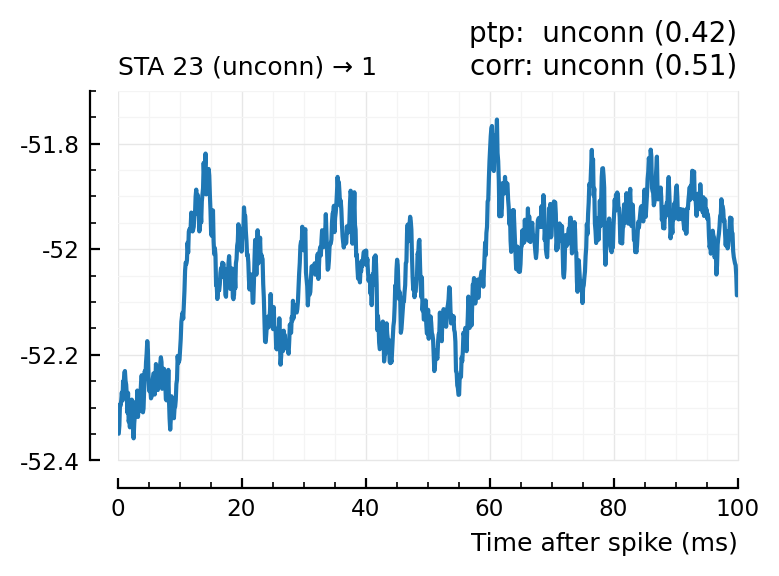
(For comparison, some clearly unconnecteds):

plotcase(23);
plotcase(25);

../_images/2022-09-09__Conntest_with_template_matching_65_0.png

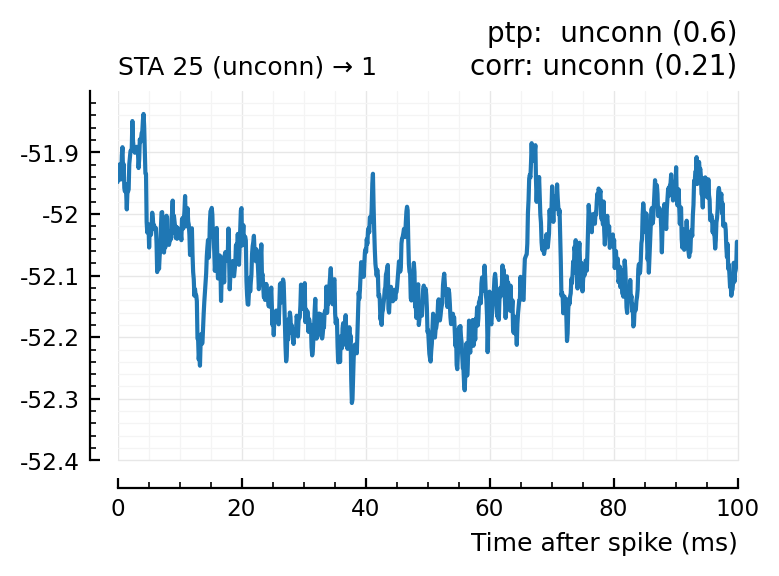
../_images/2022-09-09__Conntest_with_template_matching_65_1.png

Now, apply this to all recorded postsynaptic neurons.

For that, we’ll add this connection test (and connection type test) to our codebase.

Copy-and-edit from codebase¶

(These functions use external var avgSTA).

# Renaming some existing funcs 
STA_shuffle_test             = VoltoMapSim.test_connection
test_conn_using_ptp_and_area = VoltoMapSim.test_connection_and_type;

function test_conn_using_corr(v, spikes, p::ExpParams)
    @unpack α = p.evaluation
    STA = calc_STA(v, spikes, p)
    corr = cor(STA, avgSTA)
    if (corr > 0) test_stat = STA -> cor(STA, avgSTA)
    else          test_stat = STA -> -cor(STA, avgSTA) end
        # have to use anonymous funcs here: https://stackoverflow.com/a/65660721/2611913
    pval = STA_shuffle_test(v, spikes, p, test_stat)
    if     (pval ≥ α)  predtype = :unconn
    elseif (corr > 0)  predtype = :exc
    else               predtype = :inh end
    return predtype, (; pval, corr)
end;

function evaluate_conntest_perf_v3(s, m, p::ExperimentParams, verbose = true, testfunc = test_conn_using_ptp_and_area)
    # s = augmented simdata
    # m = postsynaptic neuron ID
    # testfunc is a function taking (voltage, spikes, p) and 
    #   returning (predicted_type::Symbol, extra_info::NamedTuple)
    @unpack N_tested_presyn, rngseed = p.evaluation;
    resetrng!(rngseed)
    function get_IDs_labels(IDs, label)
        # Example output: `[(3, :exc), (5, :exc), (12, :exc), …]`.
        N = min(length(IDs), N_tested_presyn)
        IDs_sample = sample(IDs, N, replace = false, ordered = true)
        return zip(IDs_sample, fill(label, N))
    end
    ii = s.input_info[m]
    IDs_labels = chain(
        get_IDs_labels(ii.exc_inputs, :exc),
        get_IDs_labels(ii.inh_inputs, :inh),
        get_IDs_labels(ii.unconnected_neurons, :unconn),
    ) |> collect    
    tested_neurons = DataFrame(
        input_neuron_ID = Int[],     # global ID
        real_type       = Symbol[],  # :unconn, :exc, :inh
        predicted_type  = Symbol[],  # idem
    )
    extra_infos = []
    N = length(IDs_labels)
    pbar = Progress(N, desc = "Testing connections: ", enabled = verbose, dt = 400ms)
    for (n, label) in IDs_labels
        predtype, extra_info = testfunc(ii.v, s.spike_times[n], p)
        row = (
            input_neuron_ID = n,
            real_type       = label,
            predicted_type  = predtype,
        )
        push!(tested_neurons, Dict(pairs(row)))
        push!(extra_infos, extra_info)
        next!(pbar)
    end
    tn = tested_neurons
    # Add `extra_info` columns to table
    colnames = keys(first(extra_infos))
    for colname in colnames
        tn[!, colname] = [tup[colname] for tup in extra_infos]
    end
    # Calculate detection rates (false positive and true positive rates)
    det_rate(t) = count((tn.real_type .== t) .& (tn.predicted_type .== t)) / count(tn.real_type .== t)
    detection_rates = (
        TPR_exc = det_rate(:exc),
        TPR_inh = det_rate(:inh),
        FPR = 1 - det_rate(:unconn),
    )
    return perf = (; tested_neurons, detection_rates)
end

cached_conntest_eval_v3(s, m, p; verbose = true, testfunc = test_conn_using_ptp_and_area) =
    cached(evaluate_conntest_perf_v3, [s, m, p, verbose, testfunc]; key = [m, p, string(testfunc)], verbose);

perf = cached_conntest_eval_v3(s, 1, p; testfunc = test_conn_using_corr)
perf.detection_rates

Testing connections: 100%|██████████████████████████████| Time: 0:00:31
Saving output at `C:\Users\tfiers\.phdcache\datamodel v2 (net)\evaluate_conntest_perf_v3\a17be8fa72748bbc.jld2` … done (6.2 s)

(TPR_exc = 0.885, TPR_inh = 1, FPR = 0.125)

# evaluate_conntest_perf_v3(s, 1, p, true, test_conn_using_corr)

Cool, works (and we now get our final improvement for neuron 1, with the new exc/inh decider too). Peak-to-peak and area performance (from above):
(TPR_exc = 0.615, TPR_inh = 0.9, FPR = 0.125)

Now apply to all 50 recorded postsynaptic neurons

Conntest all recorded neurons¶

using Base.Threads
detrates_corr = Dict()
recorded_neurons = p.sim.network.record_v
pbar = Progress(length(recorded_neurons))
@threads for m in recorded_neurons
    perf = cached_conntest_eval_v3(s, m, p, verbose = false, testfunc = test_conn_using_corr)
    detrates_corr[m] = perf.detection_rates
    next!(pbar)
end

Progress: 100%|█████████████████████████████████████████| Time: 0:12:39

(Time taken: ~13 minutes).

function statstable(funcs, df; funcnames = string.(funcs), print = true, funcs_are_rows = true)
    # Apply each function in `funcs` to each column of the given DataFrame.
    statcols = [
        fname => [f(col) for col in eachcol(df)]
        for (f, fname) in zip(funcs, funcnames)
    ]
    df = DataFrame("" => names(df), statcols...)
    if (funcs_are_rows) df = permutedims(df, 1) end
    if print
        printsimple(df, formatters = ft_printf("%.2f"), alignment = :r)
        println()
    end
    return df
end;

to_df(detrates::Dict, ids) = DataFrame([detrates[n] for n in ids])

title(groupname, ids) = "Detection rates for $groupname neurons (n = $(length(ids)))"

detrate_distplot(detrates::DataFrame, hylabel) = ydistplot(
    "Exc. inputs" => detrates.TPR_exc,
    "Inh. inputs" => detrates.TPR_inh,
    "Unconn."     => detrates.FPR;
    ylim = [0,1],
    hylabel,
    ref = p.evaluation.α,
)
detrate_distplot(detrates, ids, groupname) = detrate_distplot(to_df(detrates, ids), title(groupname, ids))

function table(detrates, ids, groupname)
    println("\n", title(groupname, ids), ":", "\n")
    statstable([mean, median], to_df(detrates, ids))
    println("\n")
end;

function call_for_both(f, detrates)
    f(detrates, exc_post, "excitatory")
    f(detrates, inh_post, "inhibitory")
end

detrate_distplots(detrates) = call_for_both(detrate_distplot, detrates)
tables(detrates)            = call_for_both(table, detrates);

exc_post = 1:40
inh_post = 801:810;

detrate_distplots(detrates_corr);

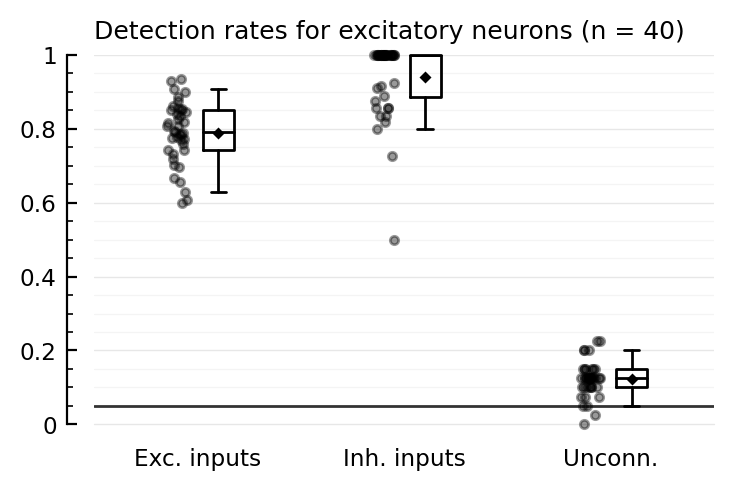
../_images/2022-09-09__Conntest_with_template_matching_83_0.png

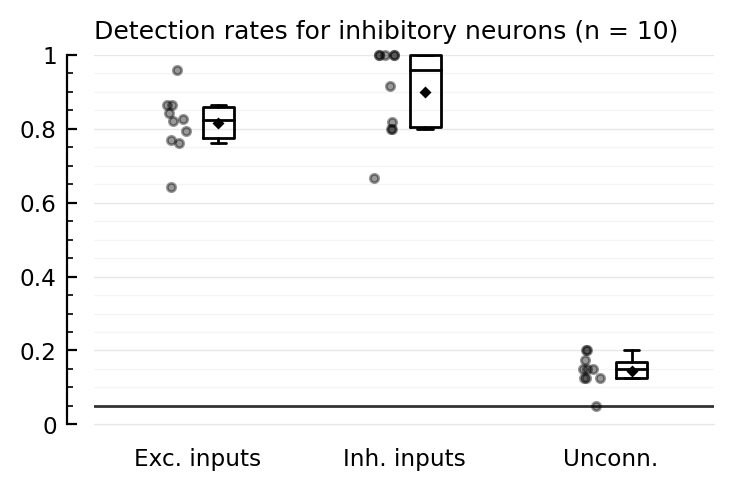
../_images/2022-09-09__Conntest_with_template_matching_83_1.png

tables(detrates_corr);

Detection rates for excitatory neurons (n = 40):

         TPR_exc  TPR_inh  FPR  
────────────────────────────────
   mean     0.79     0.94  0.12
 median     0.79     1.00  0.12



Detection rates for inhibitory neurons (n = 10):

         TPR_exc  TPR_inh  FPR  
────────────────────────────────
   mean     0.81     0.90  0.15
 median     0.82     0.96  0.15

(Could do a 95% confidence interval on e.g. median by bootstrap).

Compare with before (peak-to-peak & area-over-start)¶

detrates_ptp = Dict()
@showprogress for m in neurons
    perf = cached_conntest_eval(s, m, p, verbose = false)  # note: the previous eval func
    detrates_ptp[m] = perf.detection_rates
end

Progress: 100%|█████████████████████████████████████████| Time: 0:00:01

tables(detrates_ptp)

Detection rates for excitatory neurons (n = 40):

         TPR_exc  TPR_inh  FPR  
────────────────────────────────
   mean     0.57     0.85  0.13
 median     0.57     0.88  0.12



Detection rates for inhibitory neurons (n = 10):

         TPR_exc  TPR_inh  FPR  
────────────────────────────────
   mean     0.59     0.84  0.15
 median     0.57     0.81  0.15

Match with template but not using correlation; ref to start¶

ref_to_start(sig) = sig .- sig[1]
correspondence_with_template(STA) = mean(ref_to_start(STA) .* ref_to_start(avgSTA));

function test_conn_using_match_and_ref_to_start(v, spikes, p::ExpParams)
    @unpack α = p.evaluation
    STA = calc_STA(v, spikes, p)
    corr = correspondence_with_template(STA)
    if (corr > 0) test_stat = STA -> correspondence_with_template(STA)
    else          test_stat = STA -> -correspondence_with_template(STA) end
    pval = STA_shuffle_test(v, spikes, p, test_stat)
    if     (pval ≥ α)  predtype = :unconn
    elseif (corr > 0)  predtype = :exc
    else               predtype = :inh end
    return predtype, (; pval, corr_mV2 = corr / (mV^2))
end;

perf = cached_conntest_eval_v3(s, 1, p; testfunc = test_conn_using_match_and_ref_to_start)
perf.detection_rates

Testing connections: 100%|██████████████████████████████| Time: 0:00:30
Saving output at `C:\Users\tfiers\.phdcache\datamodel v2 (net)\evaluate_conntest_perf_v3\3d3e47c80c129767.jld2` … done

(TPR_exc = 0.769, TPR_inh = 0.9, FPR = 0.2)

Hah, so it works, but not as good as with correlation!

For all neurons:

detrates_startref = Dict()
pbar = Progress(length(recorded_neurons))
@threads for m in recorded_neurons
    perf = cached_conntest_eval_v3(s, m, p, verbose = false, testfunc = test_conn_using_match_and_ref_to_start)
    detrates_startref[m] = perf.detection_rates
    next!(pbar)
end

Progress: 100%|█████████████████████████████████████████| Time: 0:12:33

detrate_distplots(detrates_startref);

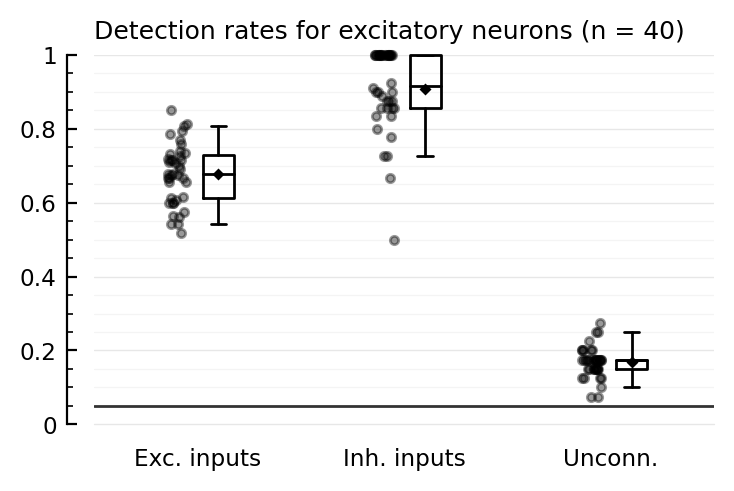
../_images/2022-09-09__Conntest_with_template_matching_95_0.png

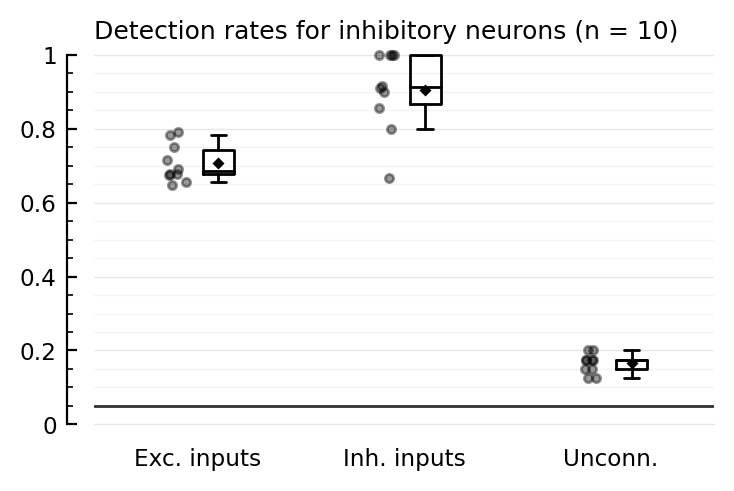
../_images/2022-09-09__Conntest_with_template_matching_95_1.png

tables(detrates_startref);

Detection rates for excitatory neurons (n = 40):

         TPR_exc  TPR_inh  FPR  
────────────────────────────────
   mean     0.68     0.91  0.17
 median     0.68     0.92  0.18



Detection rates for inhibitory neurons (n = 10):

         TPR_exc  TPR_inh  FPR  
────────────────────────────────
   mean     0.71     0.90  0.16
 median     0.69     0.91  0.18

Compare all three¶

We’ll take the median.

maindf = DataFrame(
    test_method = String[],
    postsyn_type = Symbol[],
    detrate_type = Symbol[],
    median = Float64[],
)
data = [
    "ptp-area"     => detrates_ptp,
    "corr"         => detrates_corr,
    "ref-to-start" => detrates_startref,
]
for (test_method, detrates) in data, postsyn_type in (:exc, :inh)
    group = (postsyn_type == :exc) ? exc_post : inh_post
    df = to_df(detrates, group)
    for (detrate_type, col) in pairs(eachcol(df))
        row = (; test_method, postsyn_type, detrate_type, median = median(col))
        push!(maindf, Dict(pairs(row)))
    end
end

df = copy(maindf)
sort!(df, [:detrate_type, :postsyn_type])
rename!(df, "postsyn_type" => "postsyn", "detrate_type" => "")
printsimple_(df) = printsimple(df, formatters = ft_printf("%.2f"), alignment = :r)
printsimple_(df);

 test_method   postsyn           median 
────────────────────────────────────────
     ptp-area      exc      FPR    0.12
         corr      exc      FPR    0.12
 ref-to-start      exc      FPR    0.18
     ptp-area      inh      FPR    0.15
         corr      inh      FPR    0.15
 ref-to-start      inh      FPR    0.18
     ptp-area      exc  TPR_exc    0.57
         corr      exc  TPR_exc    0.79
 ref-to-start      exc  TPR_exc    0.68
     ptp-area      inh  TPR_exc    0.57
         corr      inh  TPR_exc    0.82
 ref-to-start      inh  TPR_exc    0.69
     ptp-area      exc  TPR_inh    0.88
         corr      exc  TPR_inh    1.00
 ref-to-start      exc  TPR_inh    0.92
     ptp-area      inh  TPR_inh    0.81
         corr      inh  TPR_inh    0.96
 ref-to-start      inh  TPR_inh    0.91

ptp-area is what we did before (peak-to-peak of STA, and area-over-start to decide whether exc or inh.
corr is correlation of STA with template (which is average E→E STA)
ref-to-start is like corr, but using mean(ref(STA) .* ref(avgSTA)) where ref centers around starting value (instead of around mean).

So:

regarding FPR, corr is no better or worse than ptp-area. ref-to-start is worse.
for all TPRs, ref-to-start is better than the previous ptp-area, and corr is even better.

Filtering, widening, and sculpting the table to highlight the detection improvements:

using DataFramesMeta

df = @chain maindf begin
    @rsubset :test_method  != "ref-to-start"                # Only keep the cor method and the old method
    @rsubset string(:detrate_type) != "FPR"                 # Only keep TPRs
    unstack(:test_method, :median)                          # Widen: make new columns with given names and vals
    @rtransform! @astable begin
        :pre    = string(:detrate_type) |> s -> last(s, 3)  # Chop off "TPR_"
        :post   = string(:postsyn_type)
        :fromto = "$(:pre) → $(:post)"
    end
    sort!(:pre)
    select("fromto"=>"", "ptp-area"=>"before", "corr"=>"after")
end;

Summary¶

println("Median detection rate:\n")
printsimple_(df)

Median detection rate:

            before  after 
──────────────────────────
 exc → exc    0.57   0.79
 exc → inh    0.57   0.82
 inh → exc    0.88   1.00
 inh → inh    0.81   0.96

(And median FPRs stay the same).

Significant improvement.

Still, 1 out of 5 exc inputs still not detected (before was 2 out of 5).

Looking at their STAs though (101 and 33 (here), and 132 (here above)), it makes sense they’re not detected: the STAs look like noise. Still, why do these inputs have a weaker STA?

Also, we’re still cheating (with avgSTA as template to correlate with). Now time to play fair and fit a func.
How much of improvement will remain :p

Voltage-to-Wiring Sim

2022-09-09 • Connection test using template matching

Contents