2022-10-04 • Use faster curve fit for connection inference¶

As we saw in the previous notebook, we can get away with way fewer Levenberg-Marquardt steps (see here for more on that algo) to get a decent fit: the difference in fit quality between 10 and the default ~350 iterations is not that big.

Imports¶

using MyToolbox

@time_imports using VoltoMapSim

[ Info: Precompiling VoltoMapSim [f713100b-c48c-421a-b480-5fcb4c589a9e]
[ Info: Skipping precompilation since __precompile__(false). Importing VoltoMapSim [f713100b-c48c-421a-b480-5fcb4c589a9e].
[ Info: Precompiling Sciplotlib [61be95e5-9550-4d5f-a203-92a5acbc3116]
[ Info: Running Sciplotlib._precompile_
   1072.4 ms  Unitful
   1752.6 ms  Sciplotlib 51.23% compilation time
[ Info: Precompiling LsqFit [2fda8390-95c7-5789-9bda-21331edee243]
     25.5 ms  FiniteDiff 34.90% compilation time
     14.9 ms  NLSolversBase
      6.2 ms  LsqFit

The faster modelling code has been consolidated in the codebase (src/infer/model_STA.jl).

Params¶

p = get_params(
    duration = 10minutes,
    p_conn = 0.04,
    g_EE = 1, g_EI = 1, g_IE = 4, g_II = 4,
    ext_current = Normal(-0.5 * pA/√seconds, 5 * pA/√seconds),
    E_inh = -80 * mV,
    record_v = [1:40; 801:810],
);

Load STA’s¶

Load all STA’s¶

Skip this section if you want just one.

out = cached_STAs(p);

Loading cached output from `C:\Users\tfiers\.phdcache\calc_all_STAs\b9353bdd11d8b8cb.jld2` … done (16.9 s)

(ct, STAs, shuffled_STAs) = out;

α = 0.05 
conns = ct.pre .=> ct.post
example_conn(typ) = conns[findfirst(ct.conntype .== typ)]
conn = example_conn(:exc)  # 139 => 1

139 => 1

STA = copy(STAs[conn]);

Load 1 STA¶

path = cachepath("2022-10-04__inspect_curve_fit", "STA");

# savecache(path, STA);

# using SnoopCompile
# tinf = @snoopi_deep loadcache(path);

@time STA = loadcache(path);

Test one¶

fit, model = STA_modelling_funcs(p);

@time fit(STA, maxIter=10);  # compile

 27.393178 seconds (23.28 M allocations: 1.119 GiB, 14.36% gc time, 99.67% compilation time: 0% of which was recompilation)

fitfunc = fit $ (; maxIter = 10)
testfunc = modelfit_test $ (; modelling_funcs = (fitfunc, model))
test_conn(testfunc, STAs[conn], shuffled_STAs[conn])

(predtype = :exc, pval = 0.01, pval_type = "<", Eness = 0.379)

@time test_conn(testfunc, STAs[conn], shuffled_STAs[conn]);

  0.394131 seconds (10.52 k allocations: 19.963 MiB, 11.45% gc time)

This used to be 5.8 seconds (or even 50 seconds).

Test sample¶

samplesize = 100
resetrng!(1234)
i = sample(1:nrow(ct), samplesize, replace = false)
ctsample = ct[i, :];

summarize_conns_to_test(ctsample)

We test 100 putative input connections to 45 neurons.
32 of those connections are excitatory, 15 are inhibitory, and the remaining 53 are non-connections.

tc = test_conns(testfunc, ctsample, STAs, shuffled_STAs, α = 0.05);

Testing connections: 100%|██████████████████████████████| Time: 0:00:40

perftable(tc)

Tested connections: 100
		┌───────	Real type	───────┐	Precision
		`unconn`	`exc`	`inh`
┌	`unconn`	44	12	2	76%
Predicted type	`exc`	3	20	0	87%
└	`inh`	6	0	13	68%

Sensitivity		83%	62%	87%

tc[(tc.conntype .== :exc), :] 

32×8 DataFrame

7 rows omitted

Row	posttype	post	pre	conntype	predtype	pval	pval_type	Eness
	Symbol	Int64	Int64	Symbol	Symbol	Float64	String	Float64
1	exc	17	207	exc	exc	0.01	<	2
2	exc	35	171	exc	exc	0.01	<	2
3	exc	29	682	exc	unconn	0.11	=	0.075
4	exc	7	161	exc	exc	0.01	<	0.885
5	exc	39	178	exc	exc	0.02	=	0.284
6	exc	19	515	exc	exc	0.02	=	0.108
7	exc	36	648	exc	unconn	0.59	=	0.0565
8	inh	803	757	exc	exc	0.01	<	0.705
9	exc	39	352	exc	unconn	0.19	=	0.0613
10	exc	14	781	exc	unconn	0.33	=	0.263
11	exc	28	20	exc	unconn	0.95	=	0.0152
12	inh	810	98	exc	unconn	0.59	=	0.164
13	exc	36	760	exc	exc	0.01	<	1.1
&vellip;	&vellip;	&vellip;	&vellip;	&vellip;	&vellip;	&vellip;	&vellip;	&vellip;
21	exc	29	760	exc	unconn	0.28	=	0.32
22	exc	17	4	exc	unconn	0.33	=	0.0108
23	exc	1	447	exc	exc	0.01	<	1.59
24	exc	26	516	exc	exc	0.01	<	2
25	inh	806	33	exc	exc	0.01	<	0.719
26	exc	19	282	exc	unconn	0.69	=	0.242
27	inh	805	502	exc	exc	0.01	<	0.644
28	exc	25	237	exc	exc	0.04	=	0.148
29	exc	2	779	exc	exc	0.01	<	0.831
30	exc	18	770	exc	unconn	0.62	=	-0.127
31	inh	801	206	exc	exc	0.01	<	2
32	exc	6	451	exc	exc	0.01	<	0.737

(julia.exe:20956): Gdk-CRITICAL **: 23:49:46.013: gdk_seat_default_remove_tool: assertion 'tool != NULL' failed

(julia.exe:20956): Gdk-CRITICAL **: 23:49:46.942: gdk_seat_default_remove_tool: assertion 'tool != NULL' failed

(julia.exe:20956): Gdk-CRITICAL **: 23:49:46.991: gdk_seat_default_remove_tool: assertion 'tool != NULL' failed

(julia.exe:20956): Gdk-CRITICAL **: 11:26:25.302: gdk_seat_default_remove_tool: assertion 'tool != NULL' failed

(julia.exe:20956): Gdk-CRITICAL **: 11:26:26.472: gdk_seat_default_remove_tool: assertion 'tool != NULL' failed

(julia.exe:20956): Gdk-CRITICAL **: 11:26:26.626: gdk_seat_default_remove_tool: assertion 'tool != NULL' failed

plotsig(STAs[20=>28] / mV, p);
plotsig(STAs[451=>6] / mV, p);
plotsig(STAs[770=>18] / mV, p);
plotsig(STAs[33=>806] / mV, p);

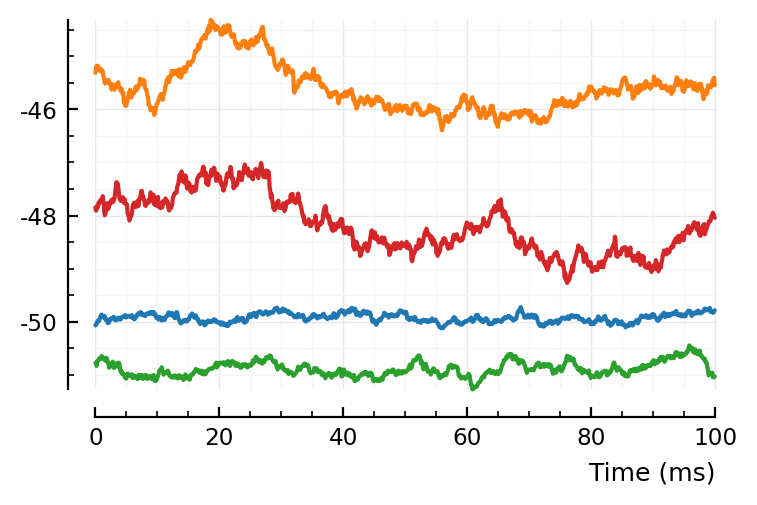
../_images/2022-10-07__Conntest_with_faster_curve_fit_33_0.png

oh ow, is this the nonlinearity of Izhikevich at play? (Weaker excitation at lower voltages). Hm or is that sth else (nb).

Voltage-to-Wiring Sim

2022-10-04 • Use faster curve fit for connection inference

Contents