Contents

2020-07-27 • Synaptic conductances

2020-07-27 • Synaptic conductances

This notebook builds on /notebooks/2020-07-06__Single_neuron_sim.

There, we used an ad-hoc solution to stimulate the neuron (namely, directly give I as input, where I is a spike train convolved with a manually defined EPSC).

Here, we use proper synaptic conductances.

Spike train

%run init.ipynb

Importing np, mpl, plt … ✔
Importing unyt … ✔
Importing code package (voltage_to_wiring_sim), as `v` … ✔
Imported * from v.util and from v.units

fix_rng_seed(55)

tg = v.TimeGrid(T=300*ms, dt=0.1*ms)

spikes = v.generate_Poisson_spike_train(tg, f_spike=30*Hz)

v.spike_train.plot(tg.t, spikes);
../_images/2020-07-27__Synaptic_conductances_4_0.png

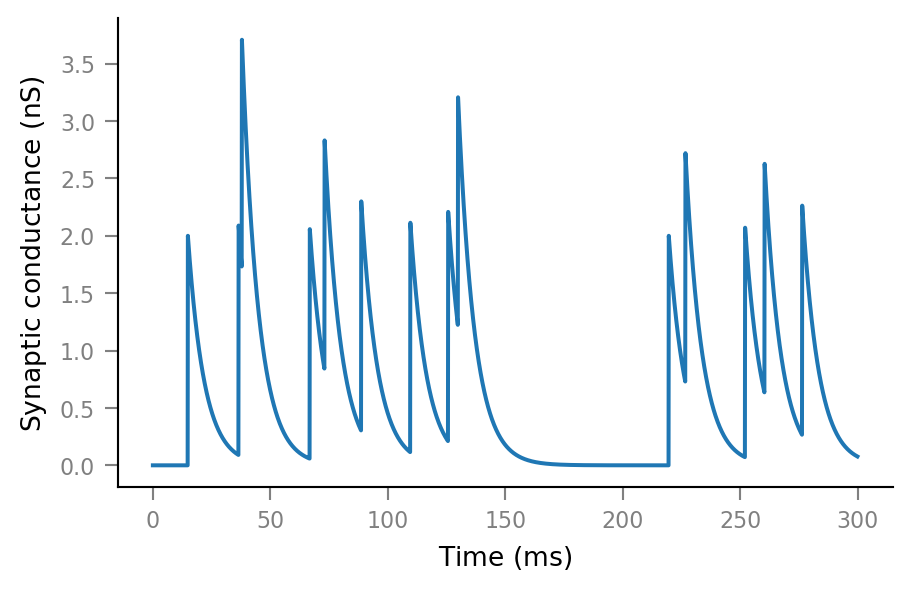
Synaptic conductance

See here for the source code that calculates the synaptic conductance.

In brief:

  • g_syn decays exponentially, with time constant τ_syn.

  • At every spike, g_syn is increased by Δg_syn.

This is e.g. how it is done in this Brian implementation of a Hodgkin-Huxley network.

Δg_syn = 2 * nS
τ_syn = 7 * ms

g_syn = v.calc_synaptic_conductance(tg, spikes, Δg_syn, τ_syn)

plt.plot(tg.t, g_syn);
../_images/2020-07-27__Synaptic_conductances_7_0.png

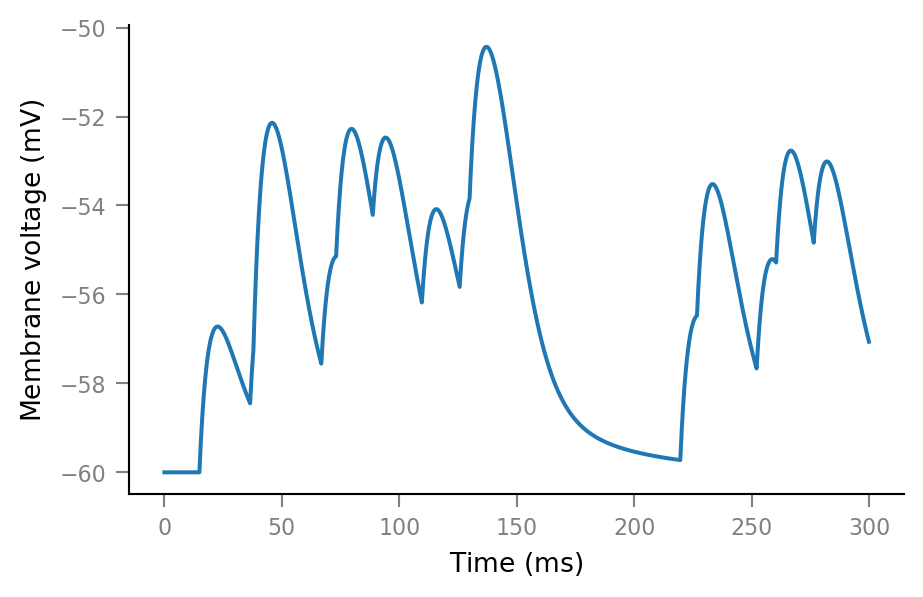
Neuron simulation

RS = v.params.cortical_RS
print(RS)

IzhikevichParams
----------------
C = 100 pF
k = 0.7 nS/mV
v_r = -60 mV
v_t = -40 mV
v_peak = 35 mV
a = 0.03 1/ms
b = -2 nS
c = -50 mV
d = 100 pA
v_syn = 0 mV

f = partial(v.simulate_izh_neuron, tg, RS)

sim = f(g_syn)

plt.plot(tg.t, sim.V_m);
../_images/2020-07-27__Synaptic_conductances_10_0.png

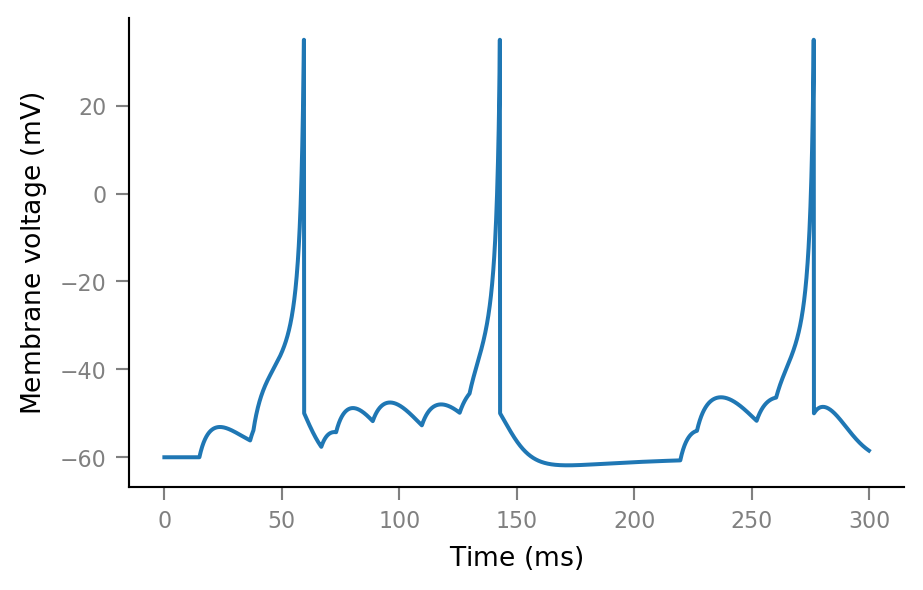
With twice as much synaptic conductance, we get spikes:

sim = f(2 * g_syn)

plt.plot(tg.t, sim.V_m);
../_images/2020-07-27__Synaptic_conductances_12_0.png 
fig, axes = plt.subplots(nrows=4, **v.figsize(aspect=2))

signals = g_syn, sim.I_syn, sim.V_m, sim.u

for i, (ax, sig) in enumerate(zip(axes, signals)):
    ax.plot(tg.t, sig)
    if i < 3:
        ax.set_xlabel(None)
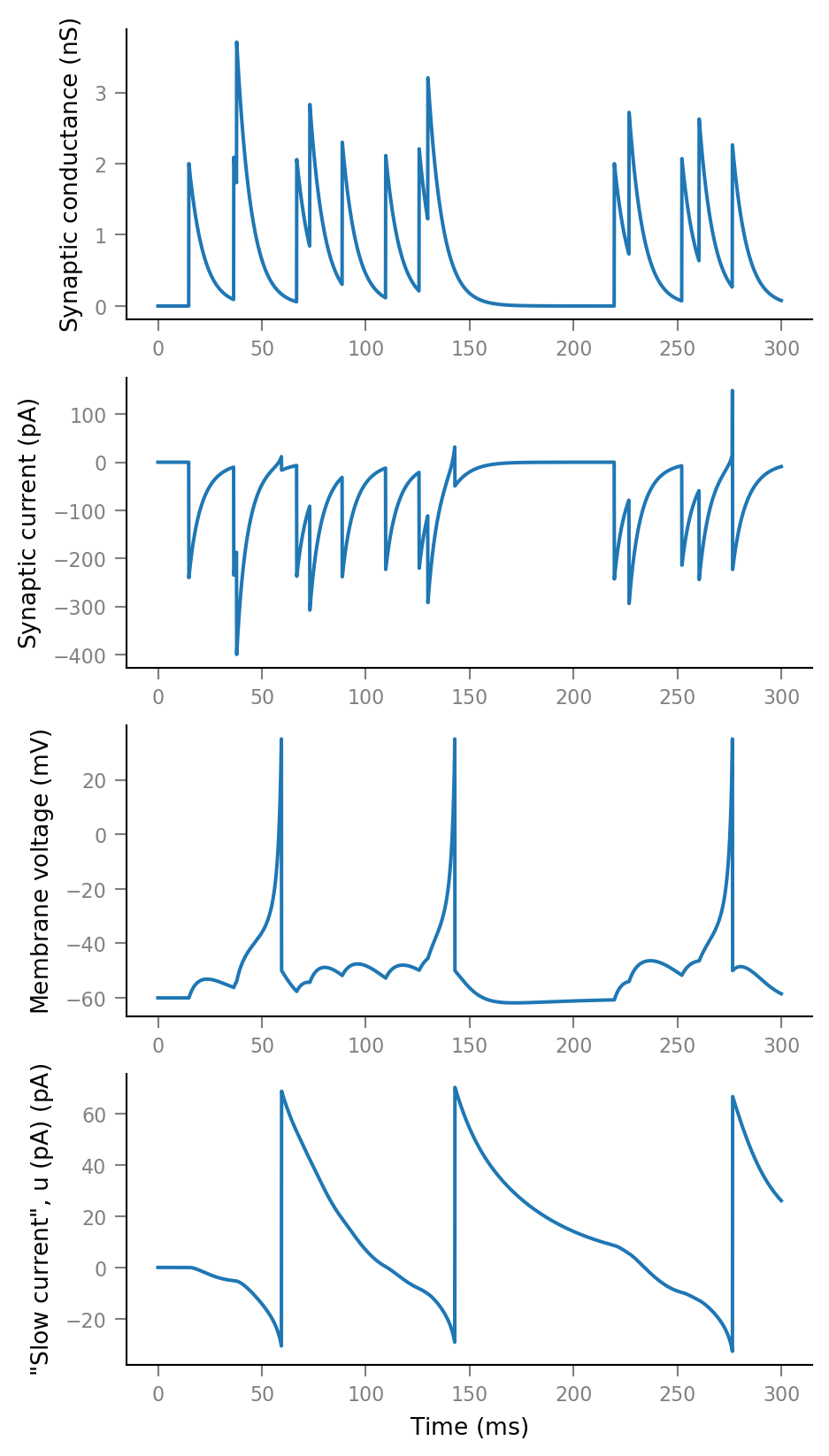
../_images/2020-07-27__Synaptic_conductances_13_0.png

Note that membrane currents, such as the synaptic current, are defined by convention as positive outward (ch 5 of Dayan-Abott). Here synaptic current flows into the neuron, hence the negative sign.

Note also the brief periods where the synaptic current is positive, whenever the membrane potential is higher than the synaptic reversal potential v_syn.

previous

2020-07-29 • Spike-triggered averaging

next

2020-07-06 • Single neuron simulation